A site for solving at least some of your technical problems...
Creating a drive mirror with LVM, including exact partition cloning
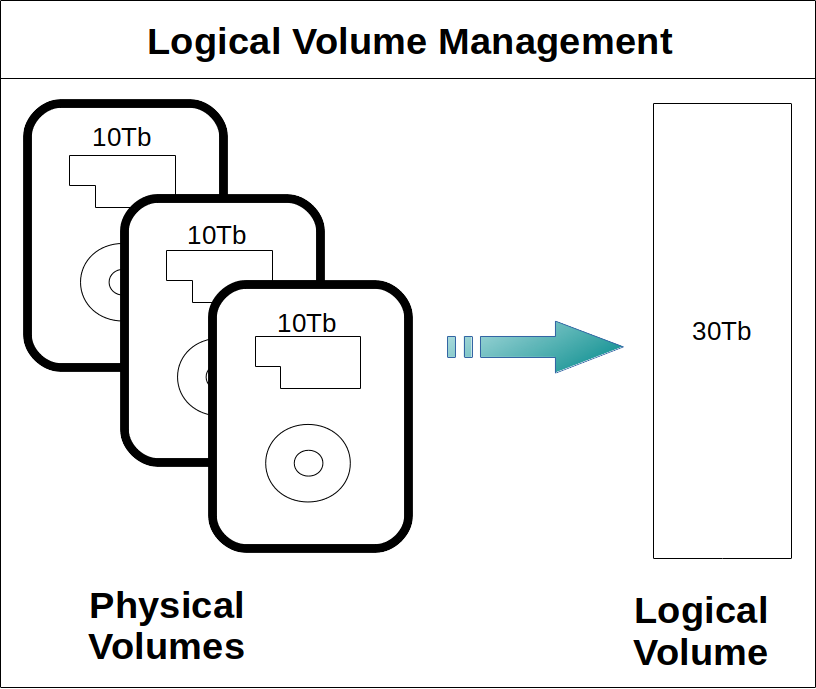
LVM today can create a mirror of your data (RAID 1) without having the need for mdraid/mdadm (or hardware raid).
I started writing this page in Nov 2012. Since then the LVM support has been improving quite a bit. making it easier and easier to group physical hard drive and setting them up in all sorts of ways (LVM now supports RAID 0, 1, 4, 5, 6, 10. It also supports the special type called "Thin" which allows you to allocate more virtual disk space than is available physically. So you could pretend you have a hard drive of 1 Eb... and add physical space as you actually really need it.
In 2012, though, I ran in a problem: I did not find any documentation that makes sense and there didn't seem to be a graphical interface that could help you with that (at least not under Ubuntu Gnome.) That changed now. RedHat has a lot of pretty good docs and we have a KDE based graphical interface available.
Anyway... at the time, I decided to spend the time because that's probably less time anyway than trying to create and maintain an md device. (I did that in the old days and it's not practical at all.)
The fact is, it is rather simple, but requires quite a bit of knowledge.
New Installations & GParted
In 2020 (but it has been a while now), when you have a brand new computer and install the hard drives for the first time, the installer offers you to create a mirror. This is much better than in the old days (befor 2012). It will setup the computer with an mdadm setup automatically and it just works.
However, this is not really what we want (well, maybe you prefer that method but then it's different than using the LVM system which is more versatil). You should either ignore the capability and install the OS on one drive and later change the settings, or use the advance features and setup the LVM then a RAID on the LVM. There is no options I've seen to do that mostly automatically.
As for partitions, by default Linux creates one root partition and one small boot partition. The boot parition is to be sure that your computer will be capable of starting up (i.e. the BIOS has to find the blocks, read them, start execution...) I strongly suggest you setup a separate /home partition too. This way you will be able to upgrade your computer without having to change the partitions at that time. (It's much harder and time consuming to change the parititions later).
If you are to use a database or other such software that save data under /var, then you may also want to have a separate partition for /var. It is also a good idea to separate the /home and /var but not as important for partitioning your devices.
The /home separate partition is expected to be an LVM partition on the one large partition GParted otherwise creates.
New Ubuntu Installation with a degraded LVM RAID1
Today, I installed Ubuntu 24.04 (it just came out!) and it took me a day (two if you include the time to do backups). It would fail in a Python script and gave you the chance to try again, but it would fail again and again. All with no real hints about what was failing.
The system I was working on had two hard drives, the second of which was dead. It would find the drive, but could not read (even less write) from the drive. So the LVM being setup as a RAID1, it was marked as degraded.
The main problem I can see with this is if you have a drive which you cannot boot from and there is a degraded LVM, you won't be able to use that drive. You'll have to find another drive, do your install and then attach that old drive again later. There is also another possibility to fix that issue: boot a Live GParted system1, reformat that drive, then reboot with the Ubuntu 24.04 installer.
Here is how you can install gparted on your Ubuntu system:
sudo apt-get install gparted gparted
The main issue with the Gnome Parted Editor is that you cannot update your active drive(s). This is true with any hard drive tool. The root and a few other partitions cannot be messed with while mounted and unmounting them is likely not possible while the system is running.
The Live CD (or USB drive) is very useful for that. You can then update your boot drive while running the Live Parted software, and finally reboot.
Since my drive was a boot drive and I still hoped I could salvage that drive2, I did not use GParted. Instead, I used the vgreduce command line.
vgreduce --removemissing --force <group name>
I then rebooted the Ubuntu 24.04 Live Server DVD and this time it worked!
Note: the Ubuntu 22.04 Live Server DVD generated the exact same issue—I thought maybe the 22.04 version would work and I could always upgrade to 24.04 next, but that failed the exact same way.
Connecting to GParted Live via SSH
Today I wanted to check a drive and get the results in a file. The GParted system has a Check feature and the results can be saved to HTML. The problem is that I could not Copy & Paste across the VirtualBox and my Host system. So... instead I set up the SSH connection.
1. Setup eth0
My system was setup to use the newer netplan system, I had to setup the interface like in the old days, easy enough, see my how to setup the IP on Ubuntu 18.04. I used the entry just below 17.10 by creating an eth0 file under /etc/network/interfaces.d. Then ran
ifup eth0
After that, ping worked as expected.
2. Setup ssh Server
The server is available by default, but it is not running. The default setup should work as is, though.
sudo systemctl start ssh
3. Change User Password
To log in, you'll need a password. I have no clue what the "user" user password is, so I changed it like so:
sudo passwd user Password: <enter your favorite password>
4. Allow Connections
The ssh service checks allowed and denied hosts as defined in
/etc/hosts.allow /etc/hosts.deny
By default, the GParted system denies everything. I added my host IP address to the hosts.deny file like so:
ALL: ALL EXCEPT localhost 10.0.0.1
Just replace 10.0.0.1 with your host IP address and that will now be allowed to connect.
Without that step you'll get error:
ssh_exchange_identification: read: Connection reset by peer
5. Test that you can connect
Now from your host computer do:
ssh -l user <ip>
That should connect and ask you for the "user" user password. (You won't be able to log in as root).
6. Copy files with scp
If you want to copy a file (i.e. the file you save earlier) then just use scp
scp user@<ip>:file.txt .
Done!
Potential Issues
If you have a firewall on your Host system, then it may block access. Make sure to open port 22 for the <ip> address of that GParted session.
If you reboot GParted, it is going to lose your changes. Everything you do there is in memory only (i.e. especialy you boot GParted from a CD, it's not going to write anything back on that CD, it only writes to memory).
Copying the Partitions Exactly
Note: having exactly the same partitions is not required with LVM. It is extremely important with /dev/md which is closer to the physical setup of your system than LVM which is much more virtual. When creating a RAID1 with LVM partitions of different sizes, the system uses the smallest partition as the size of the RAID1 volume (unless not possible if a volume is currently too small to support all the data of the other volume).
First, I wanted the partitions to be exactly the same and using fdisk did not work. It did not want to create all the partitions saying that some were overlapping others. I had to use sfdisk instead. There are the 3 commands you need:
sfdisk -d /dev/sda >partitions.txt vim partitions.txt sfdisk /dev/sdb <partitions.txt
The vim in the middle is used to edit the file and replace all /dev/sda instances with /dev/sdb (obviously, you must map that to your hard drives!) You could instead use an sed command like this:
sed -e 's/sda/sdb/' sda-partitions.txt >sdb-partitions.txt
Notice that the file names are different so your sfdisk commands need to use those different filenames.
The following is a sample partition that was converted from /dev/sda to /dev/sdb (i.e. this is AFTER the vim edit):
# partition table of /dev/sdb unit: sectors /dev/sdb1 : start= 2048, size= 497664, Id=83, bootable /dev/sdb2 : start= 501758, size=3906527234, Id= 5 /dev/sdb3 : start= 0, size= 0, Id= 0 /dev/sdb4 : start= 0, size= 0, Id= 0 /dev/sdb5 : start= 501760, size=3906527232, Id=8e
Once I had the correct partitions, off I went to create a mirror of my 1 LVM partition.
Adding the New Drive as a LVM Mirror (-m1)
Now that we have a /dev/sdb5 partition which is an exact duplicate of our /dev/sda5 partition (parametrically) we can add it to the array as a mirror.
First check what you have with a scan:
lvm> pvscan PV /dev/sda5 VG isabelle lvm2 [1.82 TiB / 132.00 MiB free] Total: 1 [1.82 TiB] / in use: 1 [1.82 TiB] / in no VG: 0 [0 ]
Assuming you just installed a system and used the default Ubuntu setup, you have one virtual group on /dev/sda5 that looks like this (drive sizes will vary though.) Here we see that the name of the virtual group is "isabelle".
You can also use the following commands to list the physical devices, the logical devices, and the groups:
lvm> pvs lvm> lvs lvm> vgs
For example, here is the output of an lvs:
lvm> lvs LV VG Attr LSize Pool Origin Data% Meta% Move Log Cpy%Sync Convert root isabelle mwi-aom--- <250.00g [root_mlog] 100.00 swap_1 isabelle -wi-ao---- <15.97g isabelle-home isabelle rwi-aor--- <1.56t 0.70
The Attr column shows us details about the logical (virtual) partition. Especially, here we see that the root partition has 'm', which means that the paritition is mirrored using the old "mirror" type. On the other hand, the isabelle-home partition uses 'r' which stands for "RAID1". I have to use the old mirror for the root because with the newer RAID1 version my computer doesn't boot at all. Using the rescue mode from my install CD was enough for me to be able to change the root from one mode to the other so I tested both many times. I was never able to boot on the "RAID1". It works each time with the "mirror" type. This is why the output of lvs looks like this on this computer.
For more details use the display version instead:
lvm> pvdisplay lvm> lvdisplay lvm> vgdisplay
If you are in a console that has limited scrolling abilities. You can use the "s" version first (i.e. lvs), then use one of those names along the "dislpay" version. For example, to see the root partition of my isabelle's array:
lvm> lvdisplay isabelle/root
We want to add the /dev/sdb5 physical device to that group. First create the physical device within LVM with:
lvm> pvcreate /dev/sdb5 Writing physical volume data to disk "/dev/sdb5" Physical volume "/dev/sdb5" successfully created
This adds the partition /dev/sdb5 to the LVM array. We can do a pvscan again and see that the new physical drive exists in the LVM system:
lvm> pvscan PV /dev/sda5 VG isabelle lvm2 [1.82 TiB / 132.00 MiB free] PV /dev/sdb5 lvm2 [1.82 TiB] Total: 2 [3.64 TiB] / in use: 1 [1.82 TiB] / in no VG: 1 [1.82 TiB]
We notice that /dev/sdb5 is not part of any "VG" (virtual group). We use the vgextend command to add it to the existing VG:
lvm> vgextend isabelle /dev/sdb5 Volume group "isabelle" successfully extended
Obviously, you want to change the name "isabelle" with the name of your VG. With Ubuntu they set it up to the name of your computer. To make sure it was properly added, we can use pvscan again:
lvm> pvscan PV /dev/sda5 VG isabelle lvm2 [1.82 TiB / 132.00 MiB free] PV /dev/sdb5 VG isabelle lvm2 [1.82 TiB / 1.82 TiB free] Total: 2 [3.64 TiB] / in use: 2 [3.64 TiB] / in no VG: 0 [0 ]
As we can see the new partition adds a lot of free space (1.82Tb free). That will be used as we create the mirror.
lvm> lvconvert -m1 /dev/isabelle/root isabelle/root: Converted: 0.0% [...snip...] isabelle/root: Converted: 100.0%
IMPORTANT NOTE: see command below which includes two additional options to place the mirror info on disk instead of the default which is in memory--BUT THIS DOES NOT APPLY TO RAID1 TYPE.
By default, the --type raid1 option is used (you can also specify it). This is a better option than --type mirror, which is now deprecated. Note that the RAID1 mode is close to instantaneous. No on the spot conversion is required. (Please see WARNING below about the types.)
If you used mirror (first letter in Attr is "m" lvs output—it was the default a while back), you can switch to raid using the lvconvert command like so:
lvm> lvconvert --type raid1 /dev/isabelle/root
If it tells you that it doesn't have enough room, use the lvreduce command to retrieve the size first. For example, if the lvconvert command tells you it needs 1 extend, you can run:
lvm> lvreduce -l -1 --resizefs /dev/isabelle/root
As proposed in the comment by Brent below, on older systems (before Ubuntu 16.04?) you probably want to use the correct mirror log (i.e. on disk instead of memory) to allow your mirroring to function between reboots:
lvm> lvconvert -m 1 --mirrorlog mirrored --alloc anywhere /dev/isabelle/root
WARNING: keep in mind that it is better to use RAID1 (--type raid) than the olf mirror feature (which is now deprecated). So you should not need to change the mirror log. Instead you automatically get rmeta sub-partitions on each device which is much better for recovery (which is otherwise not really possible without a lot of work).
Here we convert the virtual group into a mirror level 1 group (i.e. RAID1). which has the effect of duplicating the hard drives immediately—which is a problem when the partitions are nearly 2Tb! Probably about 16 hours 2 days of work! (might be because the kids were playing on the computer while it was making the copy though.) md is better here... it does that in the background!
I don't have the final details yet, but one can use the lvs command with options as below to see that:
- the mirror is indeed in place
- what drives participate
- how much of the data has been duplicated (Copy% or Cpy%Sync)
lvm> lvs -a -o +devices LV VG Attr LSize Pool Origin Data% Move Log Copy% Convert Devices root isabelle -wi-ao-- 1.80t /dev/sda5(0) swap_1 isabelle -wi-ao-- 15.97g /dev/sda5(472748)
The final output once you have a mirror looks like this:
WARNING: This output is from the old version of my array. (1) the root_log is not replicated which is BAD, (2) it uses the mirror capability instead of the new RAID one (i.e. mimage instead of rimage).
lvm> lvs -a -o +devices LV VG Attr LSize Pool Origin Data% Move Log Copy% Convert Devices root isabelle mwi-aom- 1.80t root_mlog 100.00 root_mimage_0(0),root_mimage_1(0) [root_mimage_0] isabelle iwi-aom- 1.80t /dev/sda5(0) [root_mimage_1] isabelle iwi-aom- 1.80t /dev/sdb5(0) [root_mlog] isabelle lwi-aom- 4.00m /dev/sda5(476837) swap_1 isabelle -wi-ao-- 15.97g /dev/sda5(472748)
Note that the size of swap_1 is a 1 to 1 map of the memory (these computers have a total of 16Gb of RAM.)
(Source: http://www.novell.com/support/kb/doc.php?id=7009321 from Novell)
Hopefully you understand what you've just done... so you can repeat it for each virtual partition.
Warning
One thing to keep in mind: the LVM mirror does NOT mirror your /boot partition automatically. This being said, you won't lose your data, but you won't be able to reboot unless you correctly duplicate everything. This requires the /boot and grub proper installation which is not yet covered here.
Okay, what about a GUI app.?
There is now a graphical based application you can use to run the lvm commands.
sudo apt-get install kvpm
Note: This makes use of Qt and some other KDE extensions so you'll want to avoid it if you don't want to have anything to do with the KDE.
Once installed, you can start the tool with:
kvpm
At the top you'll see a tab called Grouped. That's where you'll see RAID as one device instead of 2 or more.
The tool works properly through SSH.
Resizing an LVM partition
This is annoying! You need to unmount a partition to resize it. That's not good, is it!? I thought that LVM would work without such drawback. The problem being that you cannot resize your root partition unless you boot on a CD or in another operating system (i.e. another Ubuntu install that boot with another partition.)
This being said, LVM still has advantages. Anyway, since I could not resize my root partition, I decided to repeat my duplication the same way as the first time. So it's going to take another 2 days. 8-P
You may be interested by Running Parted to Resize your Virtualbox Drive (including fixed drives) which explains how to do a resize of a VirtualBox Drive. It may be useful to resize a standard desktop or laptop drive too.
To shrink the size of a partition, you must also make sure to reduce the size of the file system before you redice the size of the actual partition.
For more info on resizing, check this page out: https://blog.shadypixel.com/how-to-shrink-an-lvm-volume-safely/
The commands used to resize a partition (making it smaller or larger):
# If mounted, unmount first otherwise it won't work umount /mnt/<partition> # In case the LVM system is not active vgchange -ay # First fix the file system; repeat until no more errors # Note required in newer versions (2018+) since lvresize does it for us e2fsck -f /dev/[volume-group]/[logical-volume] # resize file system first if shrinking, last if enlarging # You can use T, G, M, K for size (one letter) no decimal supported # NOT REQUIRED (see Note below) #resize2fs -p /dev/[volume-group]/[logical-volume] [size] # now resize the LV partition lvreduce --resizefs -L [newlvsize] /dev/[volume-group]/[logical-volume]
Note: The lvreduce with the --resizefs command line option already applies the resize2fs command automatically. So running resize2fs seperately is not required.
The "volume-group" is the RAID or HDD name. The "logical-volume" is the partition name. Generally, I find the names under /dev/mapper and in /etc/fstab.
Remember that resizing of the file system has to be done before when shrinking and after when enlarging your partition.
Boot Fails
Today I reinstated my LVM RAID1 feature. I inadvertendly started the replication while still booted on my Live GParted OS (i.e. I ran the lvextend -m1 /path/to/group). The LVM system decided to right away make a replica of drive A on drive B. Great, except that it's going to take a total of about 3 hours... and in between, I tried to reboot and the boot failed because of a timeout. It does not mount the drive fast enough and as a concequence the boot fails with a timeout (could not find boot drive).
On my end, I'll wait another two hours until the first replication is done to reboot. I have time. But otherwise, I think that you could reduce the RAID1 (remove the second drive), reboot and then re-add the second drive. Either way it will take a while to copy all of the data, but it would still allow you to be booted in your standard system and use your software (early3) normally.
Another possible solution is to edit your GRUB_CMDLINE_LINUX parameter and add a rootdelay=... entry. Here is ano example:
edit the file "/etc/default/grub" change from: GRUB_CMDLINE_LINUX="" GRUB_CMDLINE_LINUX="rootdelay=90 nomodeset"
Of course, you would have to do that before you boot to GParted Live in order to be able to update grub with those changes so the very next time you reboot it takes that new value in account. Otherwise, you'll likely be stuck.
I did not try either this time around since I can just wait, but that's quite a gotcha.
Root Partition Died
Last night, one of my computers using LVM2 decided to set my root partition as "deprecated". Needless to say, once the root partition is deprecated, you can't boot.
As far as I'm concerned, I find that there are several issues with newer versions of Ubuntu in this situation:
- The GRUB screen does not appear anymore, that's a new (stupid if you ask me) feature which allows for a "clean looking booting experience a la MS-Windows" which is exactly why I don't like Windows (nor macos which does the exact same thing)
- The way to access GRUB is by hitting ESC like a maniac. This is totally inconsiderate. Luckily, there is still a way to revert that back to normal and get the damn thing to show up as normal. It may require you to reboot a few times to get it right. At least, I have not yet been able to get it right the first time. What that allows you to do is then boot in the recovery mode, although if your boot partition was hosed, chances that won't help you (I did not try)
- The boot process itself hides the console by showing you a nice graphic with a few dots lighting up as things boot. Neat. Just like MS-Windows (again) that means you don't see the error(s) that prevent a computer from booting. Who thought of that?! Maybe there is a keystroke to go back to the console... I'll search on that.
Here for the rant. Now, the problem today was that somehow the system decided to mark the second hard drive as missing. It's still there and works just fine, thank you. Why would LVM mark the drive missing? Well... it looks like the md software can go missing (i.e. I mirror my root partition) and when that happens the LVM marks that specific entry with the flag missing.
First I thought I'd check the file system, but e2fsck would not work if I did not already had the LVM properly mounted...
After searching for information about the situation, I finally found a message from a user who ran in a similar problem, although in his case it looks like it was right after installing the mirror system and he says he did not install madm which would have been the culprit. But you don't need to have madm if you mirror through LVM. So I'm not so sure that his reasons were correct. In any even, he had a command to retrieve the LVM configuration file that went like this:
# vgcfgbackup -f vg.cfg
This gives us the configuration of the LVM as per your current system. This includes many dates, versions, disk information with sizes, positions, flags, etc.
Looking through the file we see this line:
flags = ["MISSING"]
It tells the system the corresponding physical disk is missing and thus the logical volume can't be rebuilt on a reboot. Since this was the only sensible solution to my problem and since my second hard drive looked just fine [at the time... after a few more days, the drive disappeared to the point that I could not even enter the BIOS—the keyboards were not responsive until after the system tried to reboot; removing the second drive resolved the problem; so definitely a deffective drive in the end], I simply ran the steps that user mentioned: (1) delete the "MISSING" flag:
flags = []
and (2) restore that updated file to the LVM system with:
# vgcfgrestore -f vg.cfg tristan
For the restore I had to specify the name of the group. If you have multiple groups, you may want to specify the name to the vgcfgbackup command so when you restore it works as expected. I don't have a way to test that theory, so you're on your own if you're in that situation.
After that change, I tried a vgscan which now included the root partition and tried a mount which also worked. I did umount and ran e2fsck against the partition and it said it was clean. So I think I was all good except for that one VG configuration flag.
The following is the complete output of the vgcfgbackup command:
# Generated by LVM2 version 2.02.176(2) (2017-11-03): Mon Feb 17 11:26:52 2020
contents = "Text Format Volume Group"
version = 1
description = "vgcfgbackup -f vg.cfg"
creation_host = "tristan" # Linux tristan 4.15.0-76-generic #86-Ubuntu SMP Fri Jan 17 17:24:28 UTC 2020 x86_64
creation_time = 1581967612 # Mon Feb 17 11:26:52 2020
tristan {
id = "ntPJjD-J0JN-BtxH-OF1A-zkaP-BLbh-k1vWLh"
seqno = 41
format = "lvm2" # informational
status = ["RESIZEABLE", "READ", "WRITE"]
flags = []
extent_size = 8192 # 4 Megabytes
max_lv = 0
max_pv = 0
metadata_copies = 0
physical_volumes {
pv0 {
id = "igXHEd-yvLC-8IFs-8MDg-Tx6T-YVTa-lz57xU"
device = "/dev/sda5" # Hint only
status = ["ALLOCATABLE"]
flags = []
dev_size = 3906527232 # 1.81912 Terabytes
pe_start = 2048
pe_count = 476870 # 1.81911 Terabytes
}
pv1 {
id = "wbaVqY-EtB2-yS8p-1Eji-NoAL-j5RV-mzYdFP"
device = "/dev/sdb5" # Hint only
status = ["ALLOCATABLE"]
flags = ["MISSING"]
dev_size = 3906527232 # 1.81912 Terabytes
pe_start = 2048
pe_count = 476870 # 1.81911 Terabytes
}
}
logical_volumes {
root {
id = "1U8OpZ-OZMv-ZnRO-K26J-sKTn-EeRo-XFA1IK"
status = ["READ", "WRITE", "VISIBLE"]
flags = []
creation_time = 1354430444 # 2012-12-01 22:40:44 -0800
creation_host = "tristan"
segment_count = 1
segment1 {
start_extent = 0
extent_count = 63999 # 249.996 Gigabytes
type = "mirror"
mirror_count = 2
mirror_log = "root_mlog"
region_size = 1024
mirrors = [
"root_mimage_0", 0,
"root_mimage_1", 0
]
}
}
swap_1 {
id = "KEuNaN-IShS-ER5P-7fTi-IwD4-mHeX-aqS3WL"
status = ["READ", "WRITE", "VISIBLE"]
flags = []
creation_time = 1354430444 # 2012-12-01 22:40:44 -0800
creation_host = "tristan"
segment_count = 1
segment1 {
start_extent = 0
extent_count = 4088 # 15.9688 Gigabytes
type = "striped"
stripe_count = 1 # linear
stripes = [
"pv0", 472748
]
}
}
tristan-home {
id = "av1jII-4xV0-UmBe-vpRG-143y-sUhs-LY2ley"
status = ["READ", "WRITE", "VISIBLE"]
flags = []
creation_time = 1579119574 # 2020-01-15 12:19:34 -0800
creation_host = "tristan"
segment_count = 4
segment1 {
start_extent = 0
extent_count = 191148 # 746.672 Gigabytes
type = "striped"
stripe_count = 1 # linear
stripes = [
"pv0", 281600
]
}
segment2 {
start_extent = 191148
extent_count = 7 # 28 Megabytes
type = "striped"
stripe_count = 1 # linear
stripes = [
"pv0", 476837
]
}
segment3 {
start_extent = 191155
extent_count = 217600 # 850 Gigabytes
type = "striped"
stripe_count = 1 # linear
stripes = [
"pv0", 64000
]
}
segment4 {
start_extent = 408755
extent_count = 25 # 100 Megabytes
type = "striped"
stripe_count = 1 # linear
stripes = [
"pv0", 476845
]
}
}
root_mimage_0 {
id = "0vApwb-6YBq-JPsf-ITt1-tZG8-OXgl-1o4ALu"
status = ["READ", "WRITE"]
flags = []
creation_time = 1354523229 # 2012-12-03 00:27:09 -0800
creation_host = "tristan"
segment_count = 1
segment1 {
start_extent = 0
extent_count = 63999 # 249.996 Gigabytes
type = "striped"
stripe_count = 1 # linear
stripes = [
"pv0", 0
]
}
}
root_mimage_1 {
id = "HtsJVj-bdTV-DfEa-Im5O-XvJJ-kgrK-5pUwl2"
status = ["READ", "WRITE"]
flags = []
creation_time = 1354523229 # 2012-12-03 00:27:09 -0800
creation_host = "tristan"
segment_count = 1
segment1 {
start_extent = 0
extent_count = 63999 # 249.996 Gigabytes
type = "striped"
stripe_count = 1 # linear
stripes = [
"pv1", 0
]
}
}
root_mlog {
id = "SfTj6B-du0z-TX3c-xrY9-Y6Lr-DjLJ-k2RVKv"
status = ["READ", "WRITE"]
flags = []
creation_time = 1579570494 # 2020-01-20 17:34:54 -0800
creation_host = "ubuntu"
allocation_policy = "normal"
segment_count = 1
segment1 {
start_extent = 0
extent_count = 1 # 4 Megabytes
type = "mirror"
mirror_count = 2
region_size = 4096
mirrors = [
"root_mlog_mimage_0", 0,
"root_mlog_mimage_1", 0
]
}
}
root_mlog_mimage_0 {
id = "2xYHUD-7D8y-vi30-OcgM-ZQZu-3KX8-wQc601"
status = ["READ", "WRITE"]
flags = []
creation_time = 1579571212 # 2020-01-20 17:46:52 -0800
creation_host = "ubuntu"
segment_count = 1
segment1 {
start_extent = 0
extent_count = 1 # 4 Megabytes
type = "striped"
stripe_count = 1 # linear
stripes = [
"pv1", 472781
]
}
}
root_mlog_mimage_1 {
id = "QuUCTP-IxuA-DZeK-3AhJ-SZQk-Ti4v-phwIVh"
status = ["READ", "WRITE"]
flags = []
creation_time = 1579571212 # 2020-01-20 17:46:52 -0800
creation_host = "ubuntu"
segment_count = 1
segment1 {
start_extent = 0
extent_count = 1 # 4 Megabytes
type = "striped"
stripe_count = 1 # linear
stripes = [
"pv1", 63999
]
}
}
}
}
As I was trying to investigate, I used this command:
# vgchange -ay
from my rescue console. This told me that the root parition was not going to be available because it's just not valid (degraded, as in a physical disk is missing).
I wanted to see more, so I used the verbose command line option like so:
# vgchange -ay -vvvv > vgchange-info.txt
and I have a copy of that output below.
Here is one line of interest:
#cache/lvmcache.c:1871 lvmcache /dev/sdb5: now in VG #orphans_lvm2 (#orphans_lvm2) with 0 mda(s).
An "orphan" in a mirror (RAID1) system is a missing disk. So here we had the answer.
#lvmcmdline.c:2787 Parsing: vgchange -ay -vvvv #lvmcmdline.c:1868 Using command index 116 id vgchange_activate enum 98. #config/config.c:1468 devices/global_filter not found in config: defaulting to global_filter = [ "a|.*/|" ] #libdm-config.c:997 Setting global/locking_type to 1 #libdm-config.c:1061 Setting global/use_lvmetad to 0 #libdm-config.c:1061 Setting devices/sysfs_scan to 1 #filters/filter-sysfs.c:327 Sysfs filter initialised. #filters/filter-internal.c:77 internal filter initialised. #filters/filter-type.c:56 LVM type filter initialised. #filters/filter-usable.c:192 Usable device filter initialised. #libdm-config.c:1061 Setting devices/multipath_component_detection to 1 #filters/filter-mpath.c:291 mpath filter initialised. #filters/filter-partitioned.c:59 Partitioned filter initialised. #libdm-config.c:1061 Setting devices/md_component_detection to 1 #filters/filter-md.c:73 MD filter initialised. #libdm-config.c:1061 Setting devices/fw_raid_component_detection to 0 #filters/filter-composite.c:104 Composite filter initialised. #libdm-config.c:1061 Setting devices/ignore_suspended_devices to 0 #libdm-config.c:1061 Setting devices/ignore_lvm_mirrors to 1 #libdm-config.c:966 Setting devices/cache_dir to /run/lvm #libdm-config.c:966 Setting devices/cache_file_prefix to #libdm-config.c:975 devices/cache not found in config: defaulting to /run/lvm/.cache #filters/filter-persistent.c:368 Persistent filter initialised. #libdm-config.c:1061 Setting devices/write_cache_state to 1 #libdm-config.c:1061 Setting global/use_lvmetad to 0 #device/dev-io.c:570 Opened /run/lvm/.cache RO #device/dev-cache.c:356 /dev/block/8:17: Added to device cache (8:17) #device/dev-cache.c:1426 Using /dev/block/8:17 #device/dev-cache.c:356 /dev/block/8:33: Added to device cache (8:33) #device/dev-cache.c:1426 Using /dev/block/8:33 #device/dev-cache.c:356 /dev/mapper/tristan-tristan--home: Added to device cache (253:1) #device/dev-cache.c:1426 Using /dev/mapper/tristan-tristan--home #device/dev-cache.c:356 /dev/tristan/swap_1: Added to device cache (253:0) #device/dev-cache.c:1426 Using /dev/tristan/swap_1 #device/dev-cache.c:356 /dev/disk/by-id/ata-ST2000DM001-9YN164_W1E1W2EQ-part5: Added to device cache (8:21) #device/dev-cache.c:1426 Using /dev/disk/by-id/ata-ST2000DM001-9YN164_W1E1W2EQ-part5 #device/dev-cache.c:356 /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part5: Added to device cache (8:5) #device/dev-cache.c:1426 Using /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part5 #device/dev-cache.c:352 /dev/disk/by-uuid/82653bb1-b4a8-4fc8-968a-f7d890794775: Aliased to /dev/tristan/swap_1 in device cache (253:0) #device/dev-cache.c:1426 Using /dev/tristan/swap_1 #device/dev-cache.c:352 /dev/disk/by-id/wwn-0x5000c5005b410358-part1: Aliased to /dev/block/8:17 in device cache (preferred name) (8:17) #device/dev-cache.c:1426 Using /dev/disk/by-id/wwn-0x5000c5005b410358-part1 #device/dev-cache.c:352 /dev/block/253:1: Aliased to /dev/mapper/tristan-tristan--home in device cache (253:1) #device/dev-cache.c:1426 Using /dev/mapper/tristan-tristan--home #device/dev-cache.c:352 /dev/disk/by-label/tristan-home: Aliased to /dev/mapper/tristan-tristan--home in device cache (253:1) #device/dev-cache.c:1426 Using /dev/mapper/tristan-tristan--home #device/dev-cache.c:352 /dev/disk/by-id/dm-uuid-LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley: Aliased to /dev/mapper/tristan-tristan--home in device cache (253:1) #device/dev-cache.c:1426 Using /dev/mapper/tristan-tristan--home #device/dev-cache.c:352 /dev/disk/by-uuid/fbd197ee-5a8d-44c1-9fbf-1821ab8962d9: Aliased to /dev/mapper/tristan-tristan--home in device cache (253:1) #device/dev-cache.c:1426 Using /dev/mapper/tristan-tristan--home #device/dev-cache.c:352 /dev/block/8:5: Aliased to /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part5 in device cache (8:5) #device/dev-cache.c:1426 Using /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part5 #device/dev-cache.c:352 /dev/disk/by-id/wwn-0x50014ee2b211ce48-part5: Aliased to /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part5 in device cache (8:5) #device/dev-cache.c:1426 Using /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part5 #device/dev-cache.c:352 /dev/disk/by-id/dm-uuid-LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL: Aliased to /dev/tristan/swap_1 in device cache (253:0) #device/dev-cache.c:1426 Using /dev/tristan/swap_1 #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-1-part5: Aliased to /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part5 in device cache (8:5) #device/dev-cache.c:1426 Using /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part5 #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-2-part1: Aliased to /dev/disk/by-id/wwn-0x5000c5005b410358-part1 in device cache (8:17) #device/dev-cache.c:1426 Using /dev/disk/by-id/wwn-0x5000c5005b410358-part1 #device/dev-cache.c:352 /dev/sda5: Aliased to /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part5 in device cache (preferred name) (8:5) #device/dev-cache.c:1426 Using /dev/sda5 #device/dev-cache.c:352 /dev/sdb5: Aliased to /dev/disk/by-id/ata-ST2000DM001-9YN164_W1E1W2EQ-part5 in device cache (preferred name) (8:21) #device/dev-cache.c:1426 Using /dev/sdb5 #device/dev-cache.c:352 /dev/block/8:21: Aliased to /dev/sdb5 in device cache (8:21) #device/dev-cache.c:1426 Using /dev/sdb5 #device/dev-cache.c:352 /dev/disk/by-partuuid/000026c1-05: Aliased to /dev/sda5 in device cache (8:5) #device/dev-cache.c:1426 Using /dev/sda5 #device/dev-cache.c:352 /dev/block/253:0: Aliased to /dev/tristan/swap_1 in device cache (253:0) #device/dev-cache.c:1426 Using /dev/tristan/swap_1 #device/dev-cache.c:356 /dev/block/8:1: Added to device cache (8:1) #device/dev-cache.c:1426 Using /dev/block/8:1 #device/dev-cache.c:352 /dev/disk/by-id/wwn-0x50014ee2b211ce48-part1: Aliased to /dev/block/8:1 in device cache (preferred name) (8:1) #device/dev-cache.c:1426 Using /dev/disk/by-id/wwn-0x50014ee2b211ce48-part1 #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-4-part1: Aliased to /dev/block/8:33 in device cache (preferred name) (8:33) #device/dev-cache.c:1426 Using /dev/disk/by-path/pci-0000:00:1f.2-ata-4-part1 #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-1-part1: Aliased to /dev/disk/by-id/wwn-0x50014ee2b211ce48-part1 in device cache (8:1) #device/dev-cache.c:1426 Using /dev/disk/by-id/wwn-0x50014ee2b211ce48-part1 #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-2-part5: Aliased to /dev/sdb5 in device cache (8:21) #device/dev-cache.c:1426 Using /dev/sdb5 #device/dev-cache.c:352 /dev/disk/by-uuid/26aeef9d-738d-42b8-9f97-0d26e9744a16: Aliased to /dev/disk/by-path/pci-0000:00:1f.2-ata-4-part1 in device cache (8:33) #device/dev-cache.c:1426 Using /dev/disk/by-path/pci-0000:00:1f.2-ata-4-part1 #device/dev-cache.c:352 /dev/sda1: Aliased to /dev/disk/by-id/wwn-0x50014ee2b211ce48-part1 in device cache (preferred name) (8:1) #device/dev-cache.c:1426 Using /dev/sda1 #device/dev-cache.c:352 /dev/sdb1: Aliased to /dev/disk/by-id/wwn-0x5000c5005b410358-part1 in device cache (preferred name) (8:17) #device/dev-cache.c:1426 Using /dev/sdb1 #device/dev-cache.c:352 /dev/sdc1: Aliased to /dev/disk/by-path/pci-0000:00:1f.2-ata-4-part1 in device cache (preferred name) (8:33) #device/dev-cache.c:1426 Using /dev/sdc1 #device/dev-cache.c:352 /dev/disk/by-partuuid/000026c1-01: Aliased to /dev/sda1 in device cache (8:1) #device/dev-cache.c:1426 Using /dev/sda1 #device/dev-cache.c:352 /dev/disk/by-id/dm-name-tristan-swap_1: Aliased to /dev/tristan/swap_1 in device cache (253:0) #device/dev-cache.c:1426 Using /dev/tristan/swap_1 #device/dev-cache.c:352 /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part1: Aliased to /dev/sda1 in device cache (8:1) #device/dev-cache.c:1426 Using /dev/sda1 #device/dev-cache.c:352 /dev/disk/by-id/wwn-0x5000c5005b410358-part5: Aliased to /dev/sdb5 in device cache (8:21) #device/dev-cache.c:1426 Using /dev/sdb5 #device/dev-cache.c:352 /dev/mapper/tristan-swap_1: Aliased to /dev/tristan/swap_1 in device cache (253:0) #device/dev-cache.c:1426 Using /dev/tristan/swap_1 #device/dev-cache.c:352 /dev/dm-1: Aliased to /dev/mapper/tristan-tristan--home in device cache (253:1) #device/dev-cache.c:1426 Using /dev/mapper/tristan-tristan--home #device/dev-cache.c:352 /dev/disk/by-uuid/0dcd8225-0c85-49d7-8df7-c5298478587f: Aliased to /dev/sda1 in device cache (8:1) #device/dev-cache.c:1426 Using /dev/sda1 #device/dev-cache.c:352 /dev/tristan/tristan-home: Aliased to /dev/mapper/tristan-tristan--home in device cache (preferred name) (253:1) #device/dev-cache.c:1426 Using /dev/tristan/tristan-home #device/dev-cache.c:352 /dev/disk/by-id/dm-name-tristan-tristan--home: Aliased to /dev/tristan/tristan-home in device cache (253:1) #device/dev-cache.c:1426 Using /dev/tristan/tristan-home #device/dev-cache.c:352 /dev/disk/by-partuuid/56312451-01: Aliased to /dev/sdc1 in device cache (8:33) #device/dev-cache.c:1426 Using /dev/sdc1 #device/dev-cache.c:352 /dev/disk/by-id/ata-SanDisk_SSD_PLUS_1000GB_190529800916-part1: Aliased to /dev/sdc1 in device cache (8:33) #device/dev-cache.c:1426 Using /dev/sdc1 #device/dev-cache.c:352 /dev/disk/by-id/ata-ST2000DM001-9YN164_W1E1W2EQ-part1: Aliased to /dev/sdb1 in device cache (8:17) #device/dev-cache.c:1426 Using /dev/sdb1 #device/dev-cache.c:352 /dev/dm-0: Aliased to /dev/tristan/swap_1 in device cache (253:0) #device/dev-cache.c:1426 Using /dev/tristan/swap_1 #device/dev-cache.c:352 /dev/disk/by-id/wwn-0x5001b448b92dd659-part1: Aliased to /dev/sdc1 in device cache (8:33) #device/dev-cache.c:1426 Using /dev/sdc1 #device/dev-cache.c:356 /dev/loop6: Added to device cache (7:6) #device/dev-cache.c:356 /dev/loop4: Added to device cache (7:4) #device/dev-cache.c:356 /dev/loop2: Added to device cache (7:2) #device/dev-cache.c:356 /dev/loop0: Added to device cache (7:0) #device/dev-cache.c:356 /dev/sdb2: Added to device cache (8:18) #device/dev-cache.c:356 /dev/loop7: Added to device cache (7:7) #device/dev-cache.c:356 /dev/sdb: Added to device cache (8:16) #device/dev-cache.c:356 /dev/loop5: Added to device cache (7:5) #device/dev-cache.c:356 /dev/sdc: Added to device cache (8:32) #device/dev-cache.c:356 /dev/sr0: Added to device cache (11:0) #device/dev-cache.c:356 /dev/loop3: Added to device cache (7:3) #device/dev-cache.c:356 /dev/loop1: Added to device cache (7:1) #device/dev-cache.c:356 /dev/sda2: Added to device cache (8:2) #device/dev-cache.c:356 /dev/sda: Added to device cache (8:0) #filters/filter-persistent.c:137 Loaded persistent filter cache from /run/lvm/.cache #device/dev-io.c:625 Closed /run/lvm/.cache #libdm-config.c:966 Setting activation/activation_mode to degraded #libdm-config.c:1074 metadata/record_lvs_history not found in config: defaulting to 0 #lvmcmdline.c:2853 DEGRADED MODE. Incomplete RAID LVs will be processed. #libdm-config.c:1061 Setting activation/monitoring to 1 #lvmcmdline.c:2859 Processing: vgchange -ay -vvvv #lvmcmdline.c:2860 Command pid: 7791 #lvmcmdline.c:2861 system ID: #lvmcmdline.c:2864 O_DIRECT will be used #libdm-config.c:997 Setting global/locking_type to 1 #libdm-config.c:1061 Setting global/wait_for_locks to 1 #locking/locking.c:129 File-based locking selected. #libdm-config.c:1061 Setting global/prioritise_write_locks to 1 #libdm-config.c:966 Setting global/locking_dir to /run/lock/lvm #libdm-config.c:1061 Setting global/use_lvmlockd to 0 #libdm-config.c:975 report/output_format not found in config: defaulting to basic #libdm-config.c:1074 log/report_command_log not found in config: defaulting to 0 #toollib.c:2182 Processing each VG #toollib.c:2234 Get list of VGs on system #cache/lvmcache.c:1139 Scanning device labels #ioctl/libdm-iface.c:1848 dm version [ opencount flush ] [16384] (*1) #ioctl/libdm-iface.c:1848 dm status (253:0) [ noopencount noflush ] [16384] (*1) #device/dev-io.c:570 Opened /dev/tristan/swap_1 RO O_DIRECT #device/dev-io.c:330 /dev/tristan/swap_1: size is 33488896 sectors #device/dev-io.c:625 Closed /dev/tristan/swap_1 #device/dev-io.c:570 Opened /dev/tristan/swap_1 RO O_DIRECT #device/dev-io.c:145 /dev/tristan/swap_1: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/swap_1: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/tristan/swap_1 #device/dev-io.c:308 /dev/tristan/swap_1: using cached size 33488896 sectors #device/dev-io.c:570 Opened /dev/tristan/swap_1 RO O_DIRECT #device/dev-io.c:145 /dev/tristan/swap_1: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/swap_1: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/tristan/swap_1 #device/dev-cache.c:1536 Using /dev/tristan/swap_1 #label/label.c:286 Reading label from device /dev/tristan/swap_1 #device/dev-io.c:570 Opened /dev/tristan/swap_1 RO O_DIRECT #device/dev-io.c:145 /dev/tristan/swap_1: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/swap_1: physical block size is 4096 bytes #label/label.c:189 /dev/tristan/swap_1: No label detected #device/dev-io.c:625 Closed /dev/tristan/swap_1 #device/dev-cache.c:1536 Using /dev/sda1 #label/label.c:286 Reading label from device /dev/sda1 #device/dev-io.c:570 Opened /dev/sda1 RO O_DIRECT #device/dev-io.c:145 /dev/sda1: block size is 4096 bytes #device/dev-io.c:156 /dev/sda1: physical block size is 4096 bytes #label/label.c:189 /dev/sda1: No label detected #device/dev-io.c:625 Closed /dev/sda1 #ioctl/libdm-iface.c:1848 dm status (253:1) [ noopencount noflush ] [16384] (*1) #device/dev-io.c:570 Opened /dev/tristan/tristan-home RO O_DIRECT #device/dev-io.c:330 /dev/tristan/tristan-home: size is 3348725760 sectors #device/dev-io.c:625 Closed /dev/tristan/tristan-home #device/dev-io.c:570 Opened /dev/tristan/tristan-home RO O_DIRECT #device/dev-io.c:145 /dev/tristan/tristan-home: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/tristan-home: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/tristan/tristan-home #device/dev-io.c:308 /dev/tristan/tristan-home: using cached size 3348725760 sectors #device/dev-io.c:570 Opened /dev/tristan/tristan-home RO O_DIRECT #device/dev-io.c:145 /dev/tristan/tristan-home: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/tristan-home: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/tristan/tristan-home #device/dev-cache.c:1536 Using /dev/tristan/tristan-home #label/label.c:286 Reading label from device /dev/tristan/tristan-home #device/dev-io.c:570 Opened /dev/tristan/tristan-home RO O_DIRECT #device/dev-io.c:145 /dev/tristan/tristan-home: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/tristan-home: physical block size is 4096 bytes #label/label.c:189 /dev/tristan/tristan-home: No label detected #device/dev-io.c:625 Closed /dev/tristan/tristan-home #device/dev-cache.c:1536 Using /dev/sda5 #label/label.c:286 Reading label from device /dev/sda5 #device/dev-io.c:570 Opened /dev/sda5 RO O_DIRECT #device/dev-io.c:145 /dev/sda5: block size is 4096 bytes #device/dev-io.c:156 /dev/sda5: physical block size is 4096 bytes #label/label.c:167 /dev/sda5: lvm2 label detected at sector 1 #cache/lvmcache.c:1871 lvmcache /dev/sda5: now in VG #orphans_lvm2 (#orphans_lvm2) with 0 mda(s). #format_text/text_label.c:422 /dev/sda5: PV header extension version 2 found #format_text/format-text.c:1260 /dev/sda5: Found metadata at 174080 size 3722 (in area at 4096 size 1044480) for tristan (ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh) #cache/lvmcache.c:522 lvmcache has no info for vgname "tristan" with VGID ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh. #cache/lvmcache.c:522 lvmcache has no info for vgname "tristan". #cache/lvmcache.c:1871 lvmcache /dev/sda5: now in VG tristan with 1 mda(s). #cache/lvmcache.c:1635 lvmcache /dev/sda5: VG tristan: set VGID to ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh. #cache/lvmcache.c:1908 lvmcache /dev/sda5: VG tristan: set creation host to ubuntu. #cache/lvmcache.c:1967 lvmcache /dev/sda5: VG tristan: stored metadata checksum 0x1223dbb1 with size 3722. #device/dev-io.c:625 Closed /dev/sda5 #device/dev-cache.c:1536 Using /dev/sdb1 #label/label.c:286 Reading label from device /dev/sdb1 #device/dev-io.c:570 Opened /dev/sdb1 RO O_DIRECT #device/dev-io.c:145 /dev/sdb1: block size is 4096 bytes #device/dev-io.c:156 /dev/sdb1: physical block size is 4096 bytes #label/label.c:189 /dev/sdb1: No label detected #device/dev-io.c:625 Closed /dev/sdb1 #device/dev-cache.c:1536 Using /dev/sdb5 #label/label.c:286 Reading label from device /dev/sdb5 #device/dev-io.c:570 Opened /dev/sdb5 RO O_DIRECT #device/dev-io.c:145 /dev/sdb5: block size is 4096 bytes #device/dev-io.c:156 /dev/sdb5: physical block size is 4096 bytes #label/label.c:167 /dev/sdb5: lvm2 label detected at sector 1 #cache/lvmcache.c:1871 lvmcache /dev/sdb5: now in VG #orphans_lvm2 (#orphans_lvm2) with 0 mda(s). #format_text/text_label.c:422 /dev/sdb5: PV header extension version 2 found #format_text/format-text.c:1260 /dev/sdb5: Using cached metadata at 134144 size 3722 (in area at 4096 size 1044480) for tristan (ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh) #cache/lvmcache.c:1871 lvmcache /dev/sdb5: now in VG tristan (ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh) with 1 mda(s). #device/dev-io.c:625 Closed /dev/sdb5 #device/dev-cache.c:1536 Using /dev/sdc1 #label/label.c:286 Reading label from device /dev/sdc1 #device/dev-io.c:570 Opened /dev/sdc1 RO O_DIRECT #device/dev-io.c:145 /dev/sdc1: block size is 4096 bytes #device/dev-io.c:156 /dev/sdc1: physical block size is 512 bytes #label/label.c:189 /dev/sdc1: No label detected #device/dev-io.c:625 Closed /dev/sdc1 #cache/lvmcache.c:1153 Scanned 7 device labels #toollib.c:1944 Processing VG tristan ntPJjD-J0JN-BtxH-OF1A-zkaP-BLbh-k1vWLh #misc/lvm-flock.c:202 Locking /run/lock/lvm/V_tristan RB #misc/lvm-flock.c:100 _do_flock /run/lock/lvm/V_tristan:aux WB #misc/lvm-flock.c:47 _undo_flock /run/lock/lvm/V_tristan:aux #misc/lvm-flock.c:100 _do_flock /run/lock/lvm/V_tristan RB #metadata/metadata.c:3806 Reading VG tristan ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh #label/label.c:286 Reading label from device /dev/sda5 #device/dev-io.c:570 Opened /dev/sda5 RO O_DIRECT #device/dev-io.c:145 /dev/sda5: block size is 4096 bytes #device/dev-io.c:156 /dev/sda5: physical block size is 4096 bytes #label/label.c:167 /dev/sda5: lvm2 label detected at sector 1 #cache/lvmcache.c:1871 lvmcache /dev/sda5: now in VG #orphans_lvm2 (#orphans_lvm2) with 1 mda(s). #format_text/text_label.c:422 /dev/sda5: PV header extension version 2 found #format_text/format-text.c:1260 /dev/sda5: Using cached metadata at 174080 size 3722 (in area at 4096 size 1044480) for tristan (ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh) #cache/lvmcache.c:1871 lvmcache /dev/sda5: now in VG tristan (ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh) with 1 mda(s). #label/label.c:286 Reading label from device /dev/sdb5 #device/dev-io.c:570 Opened /dev/sdb5 RO O_DIRECT #device/dev-io.c:145 /dev/sdb5: block size is 4096 bytes #device/dev-io.c:156 /dev/sdb5: physical block size is 4096 bytes #label/label.c:167 /dev/sdb5: lvm2 label detected at sector 1 #cache/lvmcache.c:1871 lvmcache /dev/sdb5: now in VG #orphans_lvm2 (#orphans_lvm2) with 1 mda(s). #format_text/text_label.c:422 /dev/sdb5: PV header extension version 2 found #format_text/format-text.c:1260 /dev/sdb5: Using cached metadata at 134144 size 3722 (in area at 4096 size 1044480) for tristan (ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh) #cache/lvmcache.c:1871 lvmcache /dev/sdb5: now in VG tristan (ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh) with 1 mda(s). #metadata/vg.c:74 Allocated VG tristan at 0x55fd59b4c8d0. #label/label.c:281 Reading label from lvmcache for /dev/sda5 #label/label.c:281 Reading label from lvmcache for /dev/sdb5 #format_text/import_vsn1.c:597 Importing logical volume tristan/root. #format_text/import_vsn1.c:597 Importing logical volume tristan/swap_1. #format_text/import_vsn1.c:597 Importing logical volume tristan/tristan-home. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mimage_0. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mimage_1. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mlog. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mlog_mimage_0. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mlog_mimage_1. #metadata/lv_manip.c:1189 Stack tristan/root:0[0] on LV tristan/root_mimage_0:0. #metadata/lv_manip.c:746 Adding tristan/root:0 as an user of tristan/root_mimage_0. #metadata/lv_manip.c:1189 Stack tristan/root:0[1] on LV tristan/root_mimage_1:0. #metadata/lv_manip.c:746 Adding tristan/root:0 as an user of tristan/root_mimage_1. #metadata/lv_manip.c:1189 Stack tristan/root_mlog:0[0] on LV tristan/root_mlog_mimage_0:0. #metadata/lv_manip.c:746 Adding tristan/root_mlog:0 as an user of tristan/root_mlog_mimage_0. #metadata/lv_manip.c:1189 Stack tristan/root_mlog:0[1] on LV tristan/root_mlog_mimage_1:0. #metadata/lv_manip.c:746 Adding tristan/root_mlog:0 as an user of tristan/root_mlog_mimage_1. #metadata/lv_manip.c:746 Adding tristan/root:0 as an user of tristan/root_mlog. #format_text/format-text.c:558 Read tristan metadata (40) from /dev/sda5 at 174080 size 3722 #format_text/format-text.c:563 Skipped reading metadata from /dev/sdb5 at 134144 size 3722 with matching checksum. #metadata/metadata.c:4042 Cached VG tristan had incorrect PV list #metadata/vg.c:89 Freeing VG tristan at 0x55fd59b4c8d0. #libdm-config.c:1061 Setting devices/sysfs_scan to 1 #filters/filter-sysfs.c:327 Sysfs filter initialised. #filters/filter-internal.c:77 internal filter initialised. #filters/filter-type.c:56 LVM type filter initialised. #filters/filter-usable.c:192 Usable device filter initialised. #libdm-config.c:1061 Setting devices/multipath_component_detection to 1 #filters/filter-mpath.c:291 mpath filter initialised. #filters/filter-partitioned.c:59 Partitioned filter initialised. #libdm-config.c:1061 Setting devices/md_component_detection to 1 #filters/filter-md.c:73 MD filter initialised. #libdm-config.c:1061 Setting devices/fw_raid_component_detection to 0 #filters/filter-composite.c:104 Composite filter initialised. #libdm-config.c:1061 Setting devices/ignore_suspended_devices to 0 #libdm-config.c:1061 Setting devices/ignore_lvm_mirrors to 1 #libdm-config.c:966 Setting devices/cache_dir to /run/lvm #libdm-config.c:966 Setting devices/cache_file_prefix to #libdm-config.c:975 devices/cache not found in config: defaulting to /run/lvm/.cache #filters/filter-persistent.c:368 Persistent filter initialised. #libdm-config.c:1061 Setting devices/write_cache_state to 1 #libdm-config.c:1061 Setting global/use_lvmetad to 0 #filters/filter-persistent.c:51 Wiping cache of LVM-capable devices #device/dev-cache.c:352 /dev/block/11:0: Aliased to /dev/sr0 in device cache (11:0) #device/dev-cache.c:711 Path already cached /dev/block/253:0. #device/dev-cache.c:711 Path already cached /dev/block/253:1. #device/dev-cache.c:352 /dev/block/7:0: Aliased to /dev/loop0 in device cache (7:0) #device/dev-cache.c:352 /dev/block/7:1: Aliased to /dev/loop1 in device cache (7:1) #device/dev-cache.c:352 /dev/block/7:2: Aliased to /dev/loop2 in device cache (7:2) #device/dev-cache.c:352 /dev/block/7:3: Aliased to /dev/loop3 in device cache (7:3) #device/dev-cache.c:352 /dev/block/7:4: Aliased to /dev/loop4 in device cache (7:4) #device/dev-cache.c:352 /dev/block/7:5: Aliased to /dev/loop5 in device cache (7:5) #device/dev-cache.c:352 /dev/block/7:6: Aliased to /dev/loop6 in device cache (7:6) #device/dev-cache.c:352 /dev/block/7:7: Aliased to /dev/loop7 in device cache (7:7) #device/dev-cache.c:352 /dev/block/8:0: Aliased to /dev/sda in device cache (8:0) #device/dev-cache.c:711 Path already cached /dev/block/8:1. #device/dev-cache.c:352 /dev/block/8:16: Aliased to /dev/sdb in device cache (8:16) #device/dev-cache.c:711 Path already cached /dev/block/8:17. #device/dev-cache.c:352 /dev/block/8:18: Aliased to /dev/sdb2 in device cache (8:18) #device/dev-cache.c:352 /dev/block/8:2: Aliased to /dev/sda2 in device cache (8:2) #device/dev-cache.c:711 Path already cached /dev/block/8:21. #device/dev-cache.c:352 /dev/block/8:32: Aliased to /dev/sdc in device cache (8:32) #device/dev-cache.c:711 Path already cached /dev/block/8:33. #device/dev-cache.c:711 Path already cached /dev/block/8:5. #device/dev-cache.c:1071 /dev/bsg/0:0:0:0: Not a block device #device/dev-cache.c:1071 /dev/bsg/1:0:0:0: Not a block device #device/dev-cache.c:1071 /dev/bsg/2:0:0:0: Not a block device #device/dev-cache.c:1071 /dev/bsg/3:0:0:0: Not a block device #device/dev-cache.c:1071 /dev/btrfs-control: Not a block device #device/dev-cache.c:1071 /dev/bus/usb/001/001: Not a block device #device/dev-cache.c:1071 /dev/bus/usb/001/002: Not a block device #device/dev-cache.c:1071 /dev/bus/usb/002/001: Not a block device #device/dev-cache.c:1071 /dev/bus/usb/002/002: Not a block device #device/dev-cache.c:1071 /dev/bus/usb/002/003: Not a block device #device/dev-cache.c:1071 /dev/bus/usb/002/004: Not a block device #device/dev-cache.c:1071 /dev/bus/usb/002/005: Not a block device #device/dev-cache.c:352 /dev/cdrom: Aliased to /dev/sr0 in device cache (preferred name) (11:0) #device/dev-cache.c:1071 /dev/char/108:0: Not a block device #device/dev-cache.c:1071 /dev/char/10:1: Not a block device #device/dev-cache.c:1071 /dev/char/10:183: Not a block device #device/dev-cache.c:1071 /dev/char/10:184: Not a block device #device/dev-cache.c:1071 /dev/char/10:200: Not a block device #device/dev-cache.c:1071 /dev/char/10:223: Not a block device #device/dev-cache.c:1071 /dev/char/10:227: Not a block device #device/dev-cache.c:1071 /dev/char/10:228: Not a block device #device/dev-cache.c:1071 /dev/char/10:229: Not a block device #device/dev-cache.c:1071 /dev/char/10:231: Not a block device #device/dev-cache.c:1071 /dev/char/10:234: Not a block device #device/dev-cache.c:1071 /dev/char/10:236: Not a block device #device/dev-cache.c:1071 /dev/char/10:237: Not a block device #device/dev-cache.c:1071 /dev/char/10:56: Not a block device #device/dev-cache.c:1071 /dev/char/10:57: Not a block device #device/dev-cache.c:1071 /dev/char/10:58: Not a block device #device/dev-cache.c:1071 /dev/char/10:59: Not a block device #device/dev-cache.c:1071 /dev/char/10:60: Not a block device #device/dev-cache.c:1071 /dev/char/10:61: Not a block device #device/dev-cache.c:1071 /dev/char/10:62: Not a block device #device/dev-cache.c:1071 /dev/char/10:63: Not a block device #device/dev-cache.c:1071 /dev/char/13:32: Not a block device #device/dev-cache.c:1071 /dev/char/13:33: Not a block device #device/dev-cache.c:1071 /dev/char/13:63: Not a block device #device/dev-cache.c:1071 /dev/char/13:64: Not a block device #device/dev-cache.c:1071 /dev/char/13:65: Not a block device #device/dev-cache.c:1071 /dev/char/13:66: Not a block device #device/dev-cache.c:1071 /dev/char/13:67: Not a block device #device/dev-cache.c:1071 /dev/char/13:68: Not a block device #device/dev-cache.c:1071 /dev/char/13:69: Not a block device #device/dev-cache.c:1071 /dev/char/13:70: Not a block device #device/dev-cache.c:1071 /dev/char/180:0: Not a block device #device/dev-cache.c:1071 /dev/char/189:0: Not a block device #device/dev-cache.c:1071 /dev/char/189:1: Not a block device #device/dev-cache.c:1071 /dev/char/189:128: Not a block device #device/dev-cache.c:1071 /dev/char/189:129: Not a block device #device/dev-cache.c:1071 /dev/char/189:130: Not a block device #device/dev-cache.c:1071 /dev/char/189:131: Not a block device #device/dev-cache.c:1071 /dev/char/189:132: Not a block device #device/dev-cache.c:1071 /dev/char/1:1: Not a block device #device/dev-cache.c:1071 /dev/char/1:11: Not a block device #device/dev-cache.c:1071 /dev/char/1:3: Not a block device #device/dev-cache.c:1071 /dev/char/1:4: Not a block device #device/dev-cache.c:1071 /dev/char/1:5: Not a block device #device/dev-cache.c:1071 /dev/char/1:7: Not a block device #device/dev-cache.c:1071 /dev/char/1:8: Not a block device #device/dev-cache.c:1071 /dev/char/1:9: Not a block device #device/dev-cache.c:1071 /dev/char/21:0: Not a block device #device/dev-cache.c:1071 /dev/char/21:1: Not a block device #device/dev-cache.c:1071 /dev/char/21:2: Not a block device #device/dev-cache.c:1071 /dev/char/21:3: Not a block device #device/dev-cache.c:1071 /dev/char/243:0: Not a block device #device/dev-cache.c:1071 /dev/char/243:1: Not a block device #device/dev-cache.c:1071 /dev/char/243:2: Not a block device #device/dev-cache.c:1071 /dev/char/243:3: Not a block device #device/dev-cache.c:1071 /dev/char/244:0: Not a block device #device/dev-cache.c:1071 /dev/char/244:1: Not a block device #device/dev-cache.c:1071 /dev/char/246:0: Not a block device #device/dev-cache.c:1071 /dev/char/246:1: Not a block device #device/dev-cache.c:1071 /dev/char/246:2: Not a block device #device/dev-cache.c:1071 /dev/char/246:3: Not a block device #device/dev-cache.c:1071 /dev/char/249:0: Not a block device #device/dev-cache.c:1071 /dev/char/29:0: Not a block device #device/dev-cache.c:1071 /dev/char/4:0: Not a block device #device/dev-cache.c:1071 /dev/char/4:1: Not a block device #device/dev-cache.c:1071 /dev/char/4:10: Not a block device #device/dev-cache.c:1071 /dev/char/4:11: Not a block device #device/dev-cache.c:1071 /dev/char/4:12: Not a block device #device/dev-cache.c:1071 /dev/char/4:13: Not a block device #device/dev-cache.c:1071 /dev/char/4:14: Not a block device #device/dev-cache.c:1071 /dev/char/4:15: Not a block device #device/dev-cache.c:1071 /dev/char/4:16: Not a block device #device/dev-cache.c:1071 /dev/char/4:17: Not a block device #device/dev-cache.c:1071 /dev/char/4:18: Not a block device #device/dev-cache.c:1071 /dev/char/4:19: Not a block device #device/dev-cache.c:1071 /dev/char/4:2: Not a block device #device/dev-cache.c:1071 /dev/char/4:20: Not a block device #device/dev-cache.c:1071 /dev/char/4:21: Not a block device #device/dev-cache.c:1071 /dev/char/4:22: Not a block device #device/dev-cache.c:1071 /dev/char/4:23: Not a block device #device/dev-cache.c:1071 /dev/char/4:24: Not a block device #device/dev-cache.c:1071 /dev/char/4:25: Not a block device #device/dev-cache.c:1071 /dev/char/4:26: Not a block device #device/dev-cache.c:1071 /dev/char/4:27: Not a block device #device/dev-cache.c:1071 /dev/char/4:28: Not a block device #device/dev-cache.c:1071 /dev/char/4:29: Not a block device #device/dev-cache.c:1071 /dev/char/4:3: Not a block device #device/dev-cache.c:1071 /dev/char/4:30: Not a block device #device/dev-cache.c:1071 /dev/char/4:31: Not a block device #device/dev-cache.c:1071 /dev/char/4:32: Not a block device #device/dev-cache.c:1071 /dev/char/4:33: Not a block device #device/dev-cache.c:1071 /dev/char/4:34: Not a block device #device/dev-cache.c:1071 /dev/char/4:35: Not a block device #device/dev-cache.c:1071 /dev/char/4:36: Not a block device #device/dev-cache.c:1071 /dev/char/4:37: Not a block device #device/dev-cache.c:1071 /dev/char/4:38: Not a block device #device/dev-cache.c:1071 /dev/char/4:39: Not a block device #device/dev-cache.c:1071 /dev/char/4:4: Not a block device #device/dev-cache.c:1071 /dev/char/4:40: Not a block device #device/dev-cache.c:1071 /dev/char/4:41: Not a block device #device/dev-cache.c:1071 /dev/char/4:42: Not a block device #device/dev-cache.c:1071 /dev/char/4:43: Not a block device #device/dev-cache.c:1071 /dev/char/4:44: Not a block device #device/dev-cache.c:1071 /dev/char/4:45: Not a block device #device/dev-cache.c:1071 /dev/char/4:46: Not a block device #device/dev-cache.c:1071 /dev/char/4:47: Not a block device #device/dev-cache.c:1071 /dev/char/4:48: Not a block device #device/dev-cache.c:1071 /dev/char/4:49: Not a block device #device/dev-cache.c:1071 /dev/char/4:5: Not a block device #device/dev-cache.c:1071 /dev/char/4:50: Not a block device #device/dev-cache.c:1071 /dev/char/4:51: Not a block device #device/dev-cache.c:1071 /dev/char/4:52: Not a block device #device/dev-cache.c:1071 /dev/char/4:53: Not a block device #device/dev-cache.c:1071 /dev/char/4:54: Not a block device #device/dev-cache.c:1071 /dev/char/4:55: Not a block device #device/dev-cache.c:1071 /dev/char/4:56: Not a block device #device/dev-cache.c:1071 /dev/char/4:57: Not a block device #device/dev-cache.c:1071 /dev/char/4:58: Not a block device #device/dev-cache.c:1071 /dev/char/4:59: Not a block device #device/dev-cache.c:1071 /dev/char/4:6: Not a block device #device/dev-cache.c:1071 /dev/char/4:60: Not a block device #device/dev-cache.c:1071 /dev/char/4:61: Not a block device #device/dev-cache.c:1071 /dev/char/4:62: Not a block device #device/dev-cache.c:1071 /dev/char/4:63: Not a block device #device/dev-cache.c:1071 /dev/char/4:64: Not a block device #device/dev-cache.c:1071 /dev/char/4:65: Not a block device #device/dev-cache.c:1071 /dev/char/4:66: Not a block device #device/dev-cache.c:1071 /dev/char/4:67: Not a block device #device/dev-cache.c:1071 /dev/char/4:68: Not a block device #device/dev-cache.c:1071 /dev/char/4:69: Not a block device #device/dev-cache.c:1071 /dev/char/4:7: Not a block device #device/dev-cache.c:1071 /dev/char/4:70: Not a block device #device/dev-cache.c:1071 /dev/char/4:71: Not a block device #device/dev-cache.c:1071 /dev/char/4:72: Not a block device #device/dev-cache.c:1071 /dev/char/4:73: Not a block device #device/dev-cache.c:1071 /dev/char/4:74: Not a block device #device/dev-cache.c:1071 /dev/char/4:75: Not a block device #device/dev-cache.c:1071 /dev/char/4:76: Not a block device #device/dev-cache.c:1071 /dev/char/4:77: Not a block device #device/dev-cache.c:1071 /dev/char/4:78: Not a block device #device/dev-cache.c:1071 /dev/char/4:79: Not a block device #device/dev-cache.c:1071 /dev/char/4:8: Not a block device #device/dev-cache.c:1071 /dev/char/4:80: Not a block device #device/dev-cache.c:1071 /dev/char/4:81: Not a block device #device/dev-cache.c:1071 /dev/char/4:82: Not a block device #device/dev-cache.c:1071 /dev/char/4:83: Not a block device #device/dev-cache.c:1071 /dev/char/4:84: Not a block device #device/dev-cache.c:1071 /dev/char/4:85: Not a block device #device/dev-cache.c:1071 /dev/char/4:86: Not a block device #device/dev-cache.c:1071 /dev/char/4:87: Not a block device #device/dev-cache.c:1071 /dev/char/4:88: Not a block device #device/dev-cache.c:1071 /dev/char/4:89: Not a block device #device/dev-cache.c:1071 /dev/char/4:9: Not a block device #device/dev-cache.c:1071 /dev/char/4:90: Not a block device #device/dev-cache.c:1071 /dev/char/4:91: Not a block device #device/dev-cache.c:1071 /dev/char/4:92: Not a block device #device/dev-cache.c:1071 /dev/char/4:93: Not a block device #device/dev-cache.c:1071 /dev/char/4:94: Not a block device #device/dev-cache.c:1071 /dev/char/4:95: Not a block device #device/dev-cache.c:1071 /dev/char/5:0: Not a block device #device/dev-cache.c:1071 /dev/char/5:1: Not a block device #device/dev-cache.c:1071 /dev/char/5:2: Not a block device #device/dev-cache.c:1071 /dev/char/5:3: Not a block device #device/dev-cache.c:1071 /dev/char/7:0: Not a block device #device/dev-cache.c:1071 /dev/char/7:1: Not a block device #device/dev-cache.c:1071 /dev/char/7:128: Not a block device #device/dev-cache.c:1071 /dev/char/7:129: Not a block device #device/dev-cache.c:1071 /dev/char/7:130: Not a block device #device/dev-cache.c:1071 /dev/char/7:131: Not a block device #device/dev-cache.c:1071 /dev/char/7:132: Not a block device #device/dev-cache.c:1071 /dev/char/7:133: Not a block device #device/dev-cache.c:1071 /dev/char/7:134: Not a block device #device/dev-cache.c:1071 /dev/char/7:2: Not a block device #device/dev-cache.c:1071 /dev/char/7:3: Not a block device #device/dev-cache.c:1071 /dev/char/7:4: Not a block device #device/dev-cache.c:1071 /dev/char/7:5: Not a block device #device/dev-cache.c:1071 /dev/char/7:6: Not a block device #device/dev-cache.c:1071 /dev/console: Not a block device #device/dev-cache.c:1071 /dev/core: Not a block device #device/dev-cache.c:1071 /dev/cpu/microcode: Not a block device #device/dev-cache.c:1071 /dev/cpu_dma_latency: Not a block device #device/dev-cache.c:352 /dev/disk/by-id/ata-ST2000DM001-9YN164_W1E1W2EQ: Aliased to /dev/sdb in device cache (8:16) #device/dev-cache.c:711 Path already cached /dev/disk/by-id/ata-ST2000DM001-9YN164_W1E1W2EQ-part1. #device/dev-cache.c:352 /dev/disk/by-id/ata-ST2000DM001-9YN164_W1E1W2EQ-part2: Aliased to /dev/sdb2 in device cache (8:18) #device/dev-cache.c:711 Path already cached /dev/disk/by-id/ata-ST2000DM001-9YN164_W1E1W2EQ-part5. #device/dev-cache.c:352 /dev/disk/by-id/ata-SanDisk_SSD_PLUS_1000GB_190529800916: Aliased to /dev/sdc in device cache (8:32) #device/dev-cache.c:711 Path already cached /dev/disk/by-id/ata-SanDisk_SSD_PLUS_1000GB_190529800916-part1. #device/dev-cache.c:352 /dev/disk/by-id/ata-TSSTcorp_CDDVDW_SH-224BB_R8WS68DC901P49: Aliased to /dev/cdrom in device cache (11:0) #device/dev-cache.c:352 /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091: Aliased to /dev/sda in device cache (8:0) #device/dev-cache.c:711 Path already cached /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part1. #device/dev-cache.c:352 /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part2: Aliased to /dev/sda2 in device cache (8:2) #device/dev-cache.c:711 Path already cached /dev/disk/by-id/ata-WDC_WD20EARX-00PASB0_WD-WCAZAH581091-part5. #device/dev-cache.c:711 Path already cached /dev/disk/by-id/dm-name-tristan-swap_1. #device/dev-cache.c:711 Path already cached /dev/disk/by-id/dm-name-tristan-tristan--home. #device/dev-cache.c:711 Path already cached /dev/disk/by-id/dm-uuid-LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL. #device/dev-cache.c:711 Path already cached /dev/disk/by-id/dm-uuid-LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley. #device/dev-cache.c:352 /dev/disk/by-id/wwn-0x5000c5005b410358: Aliased to /dev/sdb in device cache (8:16) #device/dev-cache.c:711 Path already cached /dev/disk/by-id/wwn-0x5000c5005b410358-part1. #device/dev-cache.c:352 /dev/disk/by-id/wwn-0x5000c5005b410358-part2: Aliased to /dev/sdb2 in device cache (8:18) #device/dev-cache.c:711 Path already cached /dev/disk/by-id/wwn-0x5000c5005b410358-part5. #device/dev-cache.c:352 /dev/disk/by-id/wwn-0x50014ee2b211ce48: Aliased to /dev/sda in device cache (8:0) #device/dev-cache.c:711 Path already cached /dev/disk/by-id/wwn-0x50014ee2b211ce48-part1. #device/dev-cache.c:352 /dev/disk/by-id/wwn-0x50014ee2b211ce48-part2: Aliased to /dev/sda2 in device cache (8:2) #device/dev-cache.c:711 Path already cached /dev/disk/by-id/wwn-0x50014ee2b211ce48-part5. #device/dev-cache.c:352 /dev/disk/by-id/wwn-0x5001b448b92dd659: Aliased to /dev/sdc in device cache (8:32) #device/dev-cache.c:711 Path already cached /dev/disk/by-id/wwn-0x5001b448b92dd659-part1. #device/dev-cache.c:352 /dev/disk/by-label/CDROM: Aliased to /dev/cdrom in device cache (11:0) #device/dev-cache.c:711 Path already cached /dev/disk/by-label/tristan-home. #device/dev-cache.c:711 Path already cached /dev/disk/by-partuuid/000026c1-01. #device/dev-cache.c:352 /dev/disk/by-partuuid/000026c1-02: Aliased to /dev/sda2 in device cache (8:2) #device/dev-cache.c:711 Path already cached /dev/disk/by-partuuid/000026c1-05. #device/dev-cache.c:711 Path already cached /dev/disk/by-partuuid/56312451-01. #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-1: Aliased to /dev/sda in device cache (8:0) #device/dev-cache.c:711 Path already cached /dev/disk/by-path/pci-0000:00:1f.2-ata-1-part1. #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-1-part2: Aliased to /dev/sda2 in device cache (8:2) #device/dev-cache.c:711 Path already cached /dev/disk/by-path/pci-0000:00:1f.2-ata-1-part5. #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-2: Aliased to /dev/sdb in device cache (8:16) #device/dev-cache.c:711 Path already cached /dev/disk/by-path/pci-0000:00:1f.2-ata-2-part1. #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-2-part2: Aliased to /dev/sdb2 in device cache (8:18) #device/dev-cache.c:711 Path already cached /dev/disk/by-path/pci-0000:00:1f.2-ata-2-part5. #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-3: Aliased to /dev/cdrom in device cache (11:0) #device/dev-cache.c:352 /dev/disk/by-path/pci-0000:00:1f.2-ata-4: Aliased to /dev/sdc in device cache (8:32) #device/dev-cache.c:711 Path already cached /dev/disk/by-path/pci-0000:00:1f.2-ata-4-part1. #device/dev-cache.c:711 Path already cached /dev/disk/by-uuid/0dcd8225-0c85-49d7-8df7-c5298478587f. #device/dev-cache.c:352 /dev/disk/by-uuid/2018-04-25-20-11-06-00: Aliased to /dev/cdrom in device cache (11:0) #device/dev-cache.c:711 Path already cached /dev/disk/by-uuid/26aeef9d-738d-42b8-9f97-0d26e9744a16. #device/dev-cache.c:711 Path already cached /dev/disk/by-uuid/82653bb1-b4a8-4fc8-968a-f7d890794775. #device/dev-cache.c:711 Path already cached /dev/disk/by-uuid/fbd197ee-5a8d-44c1-9fbf-1821ab8962d9. #device/dev-cache.c:711 Path already cached /dev/dm-0. #device/dev-cache.c:711 Path already cached /dev/dm-1. #device/dev-cache.c:1071 /dev/ecryptfs: Not a block device #device/dev-cache.c:1071 /dev/fb0: Not a block device #device/dev-cache.c:1063 /dev/fd: Symbolic link to directory #device/dev-cache.c:1071 /dev/full: Not a block device #device/dev-cache.c:1071 /dev/fuse: Not a block device #device/dev-cache.c:1071 /dev/hidraw0: Not a block device #device/dev-cache.c:1071 /dev/hidraw1: Not a block device #device/dev-cache.c:1071 /dev/hidraw2: Not a block device #device/dev-cache.c:1071 /dev/hidraw3: Not a block device #device/dev-cache.c:1071 /dev/hpet: Not a block device #device/dev-cache.c:1071 /dev/hwrng: Not a block device #device/dev-cache.c:1071 /dev/input/by-id/usb-Logitech_Logitech_USB_Keyboard-event-kbd: Not a block device #device/dev-cache.c:1071 /dev/input/by-id/usb-Logitech_Logitech_USB_Keyboard-if01-event-joystick: Not a block device #device/dev-cache.c:1071 /dev/input/by-id/usb-Logitech_Logitech_USB_Keyboard-if01-joystick: Not a block device #device/dev-cache.c:1071 /dev/input/by-id/usb-SINOWEALTH_Game_Mouse-event-mouse: Not a block device #device/dev-cache.c:1071 /dev/input/by-id/usb-SINOWEALTH_Game_Mouse-if01-event-kbd: Not a block device #device/dev-cache.c:1071 /dev/input/by-id/usb-SINOWEALTH_Game_Mouse-mouse: Not a block device #device/dev-cache.c:1071 /dev/input/by-path/pci-0000:00:1d.0-usb-0:1.3:1.0-event-mouse: Not a block device #device/dev-cache.c:1071 /dev/input/by-path/pci-0000:00:1d.0-usb-0:1.3:1.0-mouse: Not a block device #device/dev-cache.c:1071 /dev/input/by-path/pci-0000:00:1d.0-usb-0:1.3:1.1-event-kbd: Not a block device #device/dev-cache.c:1071 /dev/input/by-path/pci-0000:00:1d.0-usb-0:1.4:1.0-event-kbd: Not a block device #device/dev-cache.c:1071 /dev/input/by-path/pci-0000:00:1d.0-usb-0:1.4:1.1-event-joystick: Not a block device #device/dev-cache.c:1071 /dev/input/by-path/pci-0000:00:1d.0-usb-0:1.4:1.1-joystick: Not a block device #device/dev-cache.c:1071 /dev/input/by-path/platform-i8042-serio-1-event-kbd: Not a block device #device/dev-cache.c:1071 /dev/input/event0: Not a block device #device/dev-cache.c:1071 /dev/input/event1: Not a block device #device/dev-cache.c:1071 /dev/input/event2: Not a block device #device/dev-cache.c:1071 /dev/input/event3: Not a block device #device/dev-cache.c:1071 /dev/input/event4: Not a block device #device/dev-cache.c:1071 /dev/input/event5: Not a block device #device/dev-cache.c:1071 /dev/input/event6: Not a block device #device/dev-cache.c:1071 /dev/input/mice: Not a block device #device/dev-cache.c:1071 /dev/input/mouse0: Not a block device #device/dev-cache.c:1071 /dev/input/mouse1: Not a block device #device/dev-cache.c:1071 /dev/kmsg: Not a block device #device/dev-cache.c:1071 /dev/lightnvm/control: Not a block device #device/dev-cache.c:1071 /dev/log: Not a block device #device/dev-cache.c:1071 /dev/loop-control: Not a block device #device/dev-cache.c:340 /dev/loop0: Already in device cache #device/dev-cache.c:340 /dev/loop1: Already in device cache #device/dev-cache.c:340 /dev/loop2: Already in device cache #device/dev-cache.c:340 /dev/loop3: Already in device cache #device/dev-cache.c:340 /dev/loop4: Already in device cache #device/dev-cache.c:340 /dev/loop5: Already in device cache #device/dev-cache.c:340 /dev/loop6: Already in device cache #device/dev-cache.c:340 /dev/loop7: Already in device cache #device/dev-cache.c:1071 /dev/mapper/control: Not a block device #device/dev-cache.c:711 Path already cached /dev/mapper/tristan-swap_1. #device/dev-cache.c:711 Path already cached /dev/mapper/tristan-tristan--home. #device/dev-cache.c:1071 /dev/mcelog: Not a block device #device/dev-cache.c:1071 /dev/mem: Not a block device #device/dev-cache.c:1071 /dev/memory_bandwidth: Not a block device #device/dev-cache.c:1071 /dev/net/tun: Not a block device #device/dev-cache.c:1071 /dev/network_latency: Not a block device #device/dev-cache.c:1071 /dev/network_throughput: Not a block device #device/dev-cache.c:1071 /dev/null: Not a block device #device/dev-cache.c:1071 /dev/port: Not a block device #device/dev-cache.c:1071 /dev/ppp: Not a block device #device/dev-cache.c:1071 /dev/psaux: Not a block device #device/dev-cache.c:1071 /dev/ptmx: Not a block device #device/dev-cache.c:1071 /dev/ptp0: Not a block device #device/dev-cache.c:1071 /dev/ptp1: Not a block device #device/dev-cache.c:1071 /dev/pts/0: Not a block device #device/dev-cache.c:1071 /dev/pts/ptmx: Not a block device #device/dev-cache.c:1071 /dev/random: Not a block device #device/dev-cache.c:1071 /dev/rfkill: Not a block device #device/dev-cache.c:1071 /dev/rtc: Not a block device #device/dev-cache.c:1071 /dev/rtc0: Not a block device #device/dev-cache.c:340 /dev/sda: Already in device cache #device/dev-cache.c:711 Path already cached /dev/sda1. #device/dev-cache.c:340 /dev/sda2: Already in device cache #device/dev-cache.c:711 Path already cached /dev/sda5. #device/dev-cache.c:340 /dev/sdb: Already in device cache #device/dev-cache.c:711 Path already cached /dev/sdb1. #device/dev-cache.c:340 /dev/sdb2: Already in device cache #device/dev-cache.c:711 Path already cached /dev/sdb5. #device/dev-cache.c:340 /dev/sdc: Already in device cache #device/dev-cache.c:711 Path already cached /dev/sdc1. #device/dev-cache.c:1071 /dev/sg0: Not a block device #device/dev-cache.c:1071 /dev/sg1: Not a block device #device/dev-cache.c:1071 /dev/sg2: Not a block device #device/dev-cache.c:1071 /dev/sg3: Not a block device #device/dev-cache.c:1071 /dev/snapshot: Not a block device #device/dev-cache.c:340 /dev/sr0: Already in device cache #device/dev-cache.c:1071 /dev/stderr: Not a block device #device/dev-cache.c:1071 /dev/stdin: Not a block device #device/dev-cache.c:1071 /dev/stdout: Not a block device #device/dev-cache.c:711 Path already cached /dev/tristan/swap_1. #device/dev-cache.c:711 Path already cached /dev/tristan/tristan-home. #device/dev-cache.c:1071 /dev/tty: Not a block device #device/dev-cache.c:1071 /dev/tty0: Not a block device #device/dev-cache.c:1071 /dev/tty1: Not a block device #device/dev-cache.c:1071 /dev/tty10: Not a block device #device/dev-cache.c:1071 /dev/tty11: Not a block device #device/dev-cache.c:1071 /dev/tty12: Not a block device #device/dev-cache.c:1071 /dev/tty13: Not a block device #device/dev-cache.c:1071 /dev/tty14: Not a block device #device/dev-cache.c:1071 /dev/tty15: Not a block device #device/dev-cache.c:1071 /dev/tty16: Not a block device #device/dev-cache.c:1071 /dev/tty17: Not a block device #device/dev-cache.c:1071 /dev/tty18: Not a block device #device/dev-cache.c:1071 /dev/tty19: Not a block device #device/dev-cache.c:1071 /dev/tty2: Not a block device #device/dev-cache.c:1071 /dev/tty20: Not a block device #device/dev-cache.c:1071 /dev/tty21: Not a block device #device/dev-cache.c:1071 /dev/tty22: Not a block device #device/dev-cache.c:1071 /dev/tty23: Not a block device #device/dev-cache.c:1071 /dev/tty24: Not a block device #device/dev-cache.c:1071 /dev/tty25: Not a block device #device/dev-cache.c:1071 /dev/tty26: Not a block device #device/dev-cache.c:1071 /dev/tty27: Not a block device #device/dev-cache.c:1071 /dev/tty28: Not a block device #device/dev-cache.c:1071 /dev/tty29: Not a block device #device/dev-cache.c:1071 /dev/tty3: Not a block device #device/dev-cache.c:1071 /dev/tty30: Not a block device #device/dev-cache.c:1071 /dev/tty31: Not a block device #device/dev-cache.c:1071 /dev/tty32: Not a block device #device/dev-cache.c:1071 /dev/tty33: Not a block device #device/dev-cache.c:1071 /dev/tty34: Not a block device #device/dev-cache.c:1071 /dev/tty35: Not a block device #device/dev-cache.c:1071 /dev/tty36: Not a block device #device/dev-cache.c:1071 /dev/tty37: Not a block device #device/dev-cache.c:1071 /dev/tty38: Not a block device #device/dev-cache.c:1071 /dev/tty39: Not a block device #device/dev-cache.c:1071 /dev/tty4: Not a block device #device/dev-cache.c:1071 /dev/tty40: Not a block device #device/dev-cache.c:1071 /dev/tty41: Not a block device #device/dev-cache.c:1071 /dev/tty42: Not a block device #device/dev-cache.c:1071 /dev/tty43: Not a block device #device/dev-cache.c:1071 /dev/tty44: Not a block device #device/dev-cache.c:1071 /dev/tty45: Not a block device #device/dev-cache.c:1071 /dev/tty46: Not a block device #device/dev-cache.c:1071 /dev/tty47: Not a block device #device/dev-cache.c:1071 /dev/tty48: Not a block device #device/dev-cache.c:1071 /dev/tty49: Not a block device #device/dev-cache.c:1071 /dev/tty5: Not a block device #device/dev-cache.c:1071 /dev/tty50: Not a block device #device/dev-cache.c:1071 /dev/tty51: Not a block device #device/dev-cache.c:1071 /dev/tty52: Not a block device #device/dev-cache.c:1071 /dev/tty53: Not a block device #device/dev-cache.c:1071 /dev/tty54: Not a block device #device/dev-cache.c:1071 /dev/tty55: Not a block device #device/dev-cache.c:1071 /dev/tty56: Not a block device #device/dev-cache.c:1071 /dev/tty57: Not a block device #device/dev-cache.c:1071 /dev/tty58: Not a block device #device/dev-cache.c:1071 /dev/tty59: Not a block device #device/dev-cache.c:1071 /dev/tty6: Not a block device #device/dev-cache.c:1071 /dev/tty60: Not a block device #device/dev-cache.c:1071 /dev/tty61: Not a block device #device/dev-cache.c:1071 /dev/tty62: Not a block device #device/dev-cache.c:1071 /dev/tty63: Not a block device #device/dev-cache.c:1071 /dev/tty7: Not a block device #device/dev-cache.c:1071 /dev/tty8: Not a block device #device/dev-cache.c:1071 /dev/tty9: Not a block device #device/dev-cache.c:1071 /dev/ttyS0: Not a block device #device/dev-cache.c:1071 /dev/ttyS1: Not a block device #device/dev-cache.c:1071 /dev/ttyS10: Not a block device #device/dev-cache.c:1071 /dev/ttyS11: Not a block device #device/dev-cache.c:1071 /dev/ttyS12: Not a block device #device/dev-cache.c:1071 /dev/ttyS13: Not a block device #device/dev-cache.c:1071 /dev/ttyS14: Not a block device #device/dev-cache.c:1071 /dev/ttyS15: Not a block device #device/dev-cache.c:1071 /dev/ttyS16: Not a block device #device/dev-cache.c:1071 /dev/ttyS17: Not a block device #device/dev-cache.c:1071 /dev/ttyS18: Not a block device #device/dev-cache.c:1071 /dev/ttyS19: Not a block device #device/dev-cache.c:1071 /dev/ttyS2: Not a block device #device/dev-cache.c:1071 /dev/ttyS20: Not a block device #device/dev-cache.c:1071 /dev/ttyS21: Not a block device #device/dev-cache.c:1071 /dev/ttyS22: Not a block device #device/dev-cache.c:1071 /dev/ttyS23: Not a block device #device/dev-cache.c:1071 /dev/ttyS24: Not a block device #device/dev-cache.c:1071 /dev/ttyS25: Not a block device #device/dev-cache.c:1071 /dev/ttyS26: Not a block device #device/dev-cache.c:1071 /dev/ttyS27: Not a block device #device/dev-cache.c:1071 /dev/ttyS28: Not a block device #device/dev-cache.c:1071 /dev/ttyS29: Not a block device #device/dev-cache.c:1071 /dev/ttyS3: Not a block device #device/dev-cache.c:1071 /dev/ttyS30: Not a block device #device/dev-cache.c:1071 /dev/ttyS31: Not a block device #device/dev-cache.c:1071 /dev/ttyS4: Not a block device #device/dev-cache.c:1071 /dev/ttyS5: Not a block device #device/dev-cache.c:1071 /dev/ttyS6: Not a block device #device/dev-cache.c:1071 /dev/ttyS7: Not a block device #device/dev-cache.c:1071 /dev/ttyS8: Not a block device #device/dev-cache.c:1071 /dev/ttyS9: Not a block device #device/dev-cache.c:1071 /dev/ttyprintk: Not a block device #device/dev-cache.c:1071 /dev/uinput: Not a block device #device/dev-cache.c:1071 /dev/urandom: Not a block device #device/dev-cache.c:1071 /dev/usb/hiddev0: Not a block device #device/dev-cache.c:1071 /dev/vcs: Not a block device #device/dev-cache.c:1071 /dev/vcs1: Not a block device #device/dev-cache.c:1071 /dev/vcs2: Not a block device #device/dev-cache.c:1071 /dev/vcs3: Not a block device #device/dev-cache.c:1071 /dev/vcs4: Not a block device #device/dev-cache.c:1071 /dev/vcs5: Not a block device #device/dev-cache.c:1071 /dev/vcs6: Not a block device #device/dev-cache.c:1071 /dev/vcsa: Not a block device #device/dev-cache.c:1071 /dev/vcsa1: Not a block device #device/dev-cache.c:1071 /dev/vcsa2: Not a block device #device/dev-cache.c:1071 /dev/vcsa3: Not a block device #device/dev-cache.c:1071 /dev/vcsa4: Not a block device #device/dev-cache.c:1071 /dev/vcsa5: Not a block device #device/dev-cache.c:1071 /dev/vcsa6: Not a block device #device/dev-cache.c:1071 /dev/vga_arbiter: Not a block device #device/dev-cache.c:1071 /dev/zero: Not a block device #cache/lvmcache.c:1139 Scanning device labels #device/dev-io.c:570 Opened /dev/loop0 RO O_DIRECT #device/dev-io.c:330 /dev/loop0: size is 0 sectors #filters/filter-usable.c:44 /dev/loop0: Skipping: Too small to hold a PV #device/dev-io.c:625 Closed /dev/loop0 #device/dev-io.c:570 Opened /dev/sda RO O_DIRECT #device/dev-io.c:330 /dev/sda: size is 3907029168 sectors #device/dev-io.c:625 Closed /dev/sda #device/dev-io.c:570 Opened /dev/sda RO O_DIRECT #device/dev-io.c:145 /dev/sda: block size is 4096 bytes #device/dev-io.c:156 /dev/sda: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/sda #filters/filter-partitioned.c:27 /dev/sda: Skipping: Partition table signature found #filters/filter-type.c:27 /dev/cdrom: Skipping: Unrecognised LVM device type 11 #ioctl/libdm-iface.c:1848 dm status (253:0) [ noopencount noflush ] [16384] (*1) #device/dev-io.c:570 Opened /dev/tristan/swap_1 RO O_DIRECT #device/dev-io.c:308 /dev/tristan/swap_1: using cached size 33488896 sectors #device/dev-io.c:625 Closed /dev/tristan/swap_1 #device/dev-io.c:570 Opened /dev/tristan/swap_1 RO O_DIRECT #device/dev-io.c:145 /dev/tristan/swap_1: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/swap_1: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/tristan/swap_1 #device/dev-io.c:308 /dev/tristan/swap_1: using cached size 33488896 sectors #device/dev-io.c:570 Opened /dev/tristan/swap_1 RO O_DIRECT #device/dev-io.c:145 /dev/tristan/swap_1: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/swap_1: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/tristan/swap_1 #device/dev-cache.c:1536 Using /dev/tristan/swap_1 #label/label.c:286 Reading label from device /dev/tristan/swap_1 #device/dev-io.c:570 Opened /dev/tristan/swap_1 RO O_DIRECT #device/dev-io.c:145 /dev/tristan/swap_1: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/swap_1: physical block size is 4096 bytes #label/label.c:189 /dev/tristan/swap_1: No label detected #device/dev-io.c:625 Closed /dev/tristan/swap_1 #device/dev-io.c:570 Opened /dev/loop1 RO O_DIRECT #device/dev-io.c:330 /dev/loop1: size is 0 sectors #filters/filter-usable.c:44 /dev/loop1: Skipping: Too small to hold a PV #device/dev-io.c:625 Closed /dev/loop1 #device/dev-io.c:570 Opened /dev/sda1 RO O_DIRECT #device/dev-io.c:330 /dev/sda1: size is 497664 sectors #device/dev-io.c:625 Closed /dev/sda1 #filters/filter-mpath.c:196 /dev/sda1: Device is a partition, using primary device sda for mpath component detection #device/dev-io.c:308 /dev/sda1: using cached size 497664 sectors #device/dev-io.c:570 Opened /dev/sda1 RO O_DIRECT #device/dev-io.c:145 /dev/sda1: block size is 4096 bytes #device/dev-io.c:156 /dev/sda1: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/sda1 #device/dev-cache.c:1536 Using /dev/sda1 #label/label.c:286 Reading label from device /dev/sda1 #device/dev-io.c:570 Opened /dev/sda1 RO O_DIRECT #device/dev-io.c:145 /dev/sda1: block size is 4096 bytes #device/dev-io.c:156 /dev/sda1: physical block size is 4096 bytes #label/label.c:189 /dev/sda1: No label detected #device/dev-io.c:625 Closed /dev/sda1 #ioctl/libdm-iface.c:1848 dm status (253:1) [ noopencount noflush ] [16384] (*1) #device/dev-io.c:570 Opened /dev/tristan/tristan-home RO O_DIRECT #device/dev-io.c:308 /dev/tristan/tristan-home: using cached size 3348725760 sectors #device/dev-io.c:625 Closed /dev/tristan/tristan-home #device/dev-io.c:570 Opened /dev/tristan/tristan-home RO O_DIRECT #device/dev-io.c:145 /dev/tristan/tristan-home: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/tristan-home: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/tristan/tristan-home #device/dev-io.c:308 /dev/tristan/tristan-home: using cached size 3348725760 sectors #device/dev-io.c:570 Opened /dev/tristan/tristan-home RO O_DIRECT #device/dev-io.c:145 /dev/tristan/tristan-home: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/tristan-home: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/tristan/tristan-home #device/dev-cache.c:1536 Using /dev/tristan/tristan-home #label/label.c:286 Reading label from device /dev/tristan/tristan-home #device/dev-io.c:570 Opened /dev/tristan/tristan-home RO O_DIRECT #device/dev-io.c:145 /dev/tristan/tristan-home: block size is 4096 bytes #device/dev-io.c:156 /dev/tristan/tristan-home: physical block size is 4096 bytes #label/label.c:189 /dev/tristan/tristan-home: No label detected #device/dev-io.c:625 Closed /dev/tristan/tristan-home #device/dev-io.c:570 Opened /dev/loop2 RO O_DIRECT #device/dev-io.c:330 /dev/loop2: size is 0 sectors #filters/filter-usable.c:44 /dev/loop2: Skipping: Too small to hold a PV #device/dev-io.c:625 Closed /dev/loop2 #device/dev-io.c:570 Opened /dev/sda2 RO O_DIRECT #device/dev-io.c:330 /dev/sda2: size is 2 sectors #filters/filter-usable.c:44 /dev/sda2: Skipping: Too small to hold a PV #device/dev-io.c:625 Closed /dev/sda2 #device/dev-io.c:570 Opened /dev/loop3 RO O_DIRECT #device/dev-io.c:330 /dev/loop3: size is 0 sectors #filters/filter-usable.c:44 /dev/loop3: Skipping: Too small to hold a PV #device/dev-io.c:625 Closed /dev/loop3 #device/dev-io.c:570 Opened /dev/loop4 RO O_DIRECT #device/dev-io.c:330 /dev/loop4: size is 0 sectors #filters/filter-usable.c:44 /dev/loop4: Skipping: Too small to hold a PV #device/dev-io.c:625 Closed /dev/loop4 #device/dev-io.c:570 Opened /dev/loop5 RO O_DIRECT #device/dev-io.c:330 /dev/loop5: size is 0 sectors #filters/filter-usable.c:44 /dev/loop5: Skipping: Too small to hold a PV #device/dev-io.c:625 Closed /dev/loop5 #device/dev-io.c:330 /dev/sda5: size is 3906527232 sectors #filters/filter-mpath.c:196 /dev/sda5: Device is a partition, using primary device sda for mpath component detection #device/dev-io.c:308 /dev/sda5: using cached size 3906527232 sectors #device/dev-cache.c:1536 Using /dev/sda5 #label/label.c:281 Reading label from lvmcache for /dev/sda5 #device/dev-io.c:570 Opened /dev/loop6 RO O_DIRECT #device/dev-io.c:330 /dev/loop6: size is 0 sectors #filters/filter-usable.c:44 /dev/loop6: Skipping: Too small to hold a PV #device/dev-io.c:625 Closed /dev/loop6 #device/dev-io.c:570 Opened /dev/loop7 RO O_DIRECT #device/dev-io.c:330 /dev/loop7: size is 0 sectors #filters/filter-usable.c:44 /dev/loop7: Skipping: Too small to hold a PV #device/dev-io.c:625 Closed /dev/loop7 #device/dev-io.c:570 Opened /dev/sdb RO O_DIRECT #device/dev-io.c:330 /dev/sdb: size is 3907029168 sectors #device/dev-io.c:625 Closed /dev/sdb #device/dev-io.c:570 Opened /dev/sdb RO O_DIRECT #device/dev-io.c:145 /dev/sdb: block size is 4096 bytes #device/dev-io.c:156 /dev/sdb: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/sdb #filters/filter-partitioned.c:27 /dev/sdb: Skipping: Partition table signature found #device/dev-io.c:570 Opened /dev/sdb1 RO O_DIRECT #device/dev-io.c:330 /dev/sdb1: size is 497664 sectors #device/dev-io.c:625 Closed /dev/sdb1 #filters/filter-mpath.c:196 /dev/sdb1: Device is a partition, using primary device sdb for mpath component detection #device/dev-io.c:308 /dev/sdb1: using cached size 497664 sectors #device/dev-io.c:570 Opened /dev/sdb1 RO O_DIRECT #device/dev-io.c:145 /dev/sdb1: block size is 4096 bytes #device/dev-io.c:156 /dev/sdb1: physical block size is 4096 bytes #device/dev-io.c:625 Closed /dev/sdb1 #device/dev-cache.c:1536 Using /dev/sdb1 #label/label.c:286 Reading label from device /dev/sdb1 #device/dev-io.c:570 Opened /dev/sdb1 RO O_DIRECT #device/dev-io.c:145 /dev/sdb1: block size is 4096 bytes #device/dev-io.c:156 /dev/sdb1: physical block size is 4096 bytes #label/label.c:189 /dev/sdb1: No label detected #device/dev-io.c:625 Closed /dev/sdb1 #device/dev-io.c:570 Opened /dev/sdb2 RO O_DIRECT #device/dev-io.c:330 /dev/sdb2: size is 2 sectors #filters/filter-usable.c:44 /dev/sdb2: Skipping: Too small to hold a PV #device/dev-io.c:625 Closed /dev/sdb2 #device/dev-io.c:330 /dev/sdb5: size is 3906527232 sectors #filters/filter-mpath.c:196 /dev/sdb5: Device is a partition, using primary device sdb for mpath component detection #device/dev-io.c:308 /dev/sdb5: using cached size 3906527232 sectors #device/dev-cache.c:1536 Using /dev/sdb5 #label/label.c:281 Reading label from lvmcache for /dev/sdb5 #device/dev-io.c:570 Opened /dev/sdc RO O_DIRECT #device/dev-io.c:330 /dev/sdc: size is 1953529856 sectors #device/dev-io.c:625 Closed /dev/sdc #device/dev-io.c:570 Opened /dev/sdc RO O_DIRECT #device/dev-io.c:145 /dev/sdc: block size is 4096 bytes #device/dev-io.c:156 /dev/sdc: physical block size is 512 bytes #device/dev-io.c:625 Closed /dev/sdc #filters/filter-partitioned.c:27 /dev/sdc: Skipping: Partition table signature found #device/dev-io.c:570 Opened /dev/sdc1 RO O_DIRECT #device/dev-io.c:330 /dev/sdc1: size is 1953527808 sectors #device/dev-io.c:625 Closed /dev/sdc1 #filters/filter-mpath.c:196 /dev/sdc1: Device is a partition, using primary device sdc for mpath component detection #device/dev-io.c:308 /dev/sdc1: using cached size 1953527808 sectors #device/dev-io.c:570 Opened /dev/sdc1 RO O_DIRECT #device/dev-io.c:145 /dev/sdc1: block size is 4096 bytes #device/dev-io.c:156 /dev/sdc1: physical block size is 512 bytes #device/dev-io.c:625 Closed /dev/sdc1 #device/dev-cache.c:1536 Using /dev/sdc1 #label/label.c:286 Reading label from device /dev/sdc1 #device/dev-io.c:570 Opened /dev/sdc1 RO O_DIRECT #device/dev-io.c:145 /dev/sdc1: block size is 4096 bytes #device/dev-io.c:156 /dev/sdc1: physical block size is 512 bytes #label/label.c:189 /dev/sdc1: No label detected #device/dev-io.c:625 Closed /dev/sdc1 #cache/lvmcache.c:1153 Scanned 7 device labels #metadata/vg.c:74 Allocated VG tristan at 0x55fd59b48410. #label/label.c:281 Reading label from lvmcache for /dev/sda5 #label/label.c:281 Reading label from lvmcache for /dev/sdb5 #format_text/import_vsn1.c:597 Importing logical volume tristan/root. #format_text/import_vsn1.c:597 Importing logical volume tristan/swap_1. #format_text/import_vsn1.c:597 Importing logical volume tristan/tristan-home. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mimage_0. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mimage_1. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mlog. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mlog_mimage_0. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mlog_mimage_1. #metadata/lv_manip.c:1189 Stack tristan/root:0[0] on LV tristan/root_mimage_0:0. #metadata/lv_manip.c:746 Adding tristan/root:0 as an user of tristan/root_mimage_0. #metadata/lv_manip.c:1189 Stack tristan/root:0[1] on LV tristan/root_mimage_1:0. #metadata/lv_manip.c:746 Adding tristan/root:0 as an user of tristan/root_mimage_1. #metadata/lv_manip.c:1189 Stack tristan/root_mlog:0[0] on LV tristan/root_mlog_mimage_0:0. #metadata/lv_manip.c:746 Adding tristan/root_mlog:0 as an user of tristan/root_mlog_mimage_0. #metadata/lv_manip.c:1189 Stack tristan/root_mlog:0[1] on LV tristan/root_mlog_mimage_1:0. #metadata/lv_manip.c:746 Adding tristan/root_mlog:0 as an user of tristan/root_mlog_mimage_1. #metadata/lv_manip.c:746 Adding tristan/root:0 as an user of tristan/root_mlog. #format_text/format-text.c:558 Read tristan metadata (40) from /dev/sda5 at 174080 size 3722 #format_text/format-text.c:563 Skipped reading metadata from /dev/sdb5 at 134144 size 3722 with matching checksum. #cache/lvmcache.c:1944 lvmcache /dev/sda5: VG tristan: set system_id to . #cache/lvmcache.c:202 Metadata cache: VG tristan (ntPJjD-J0JN-BtxH-OF1A-zkaP-BLbh-k1vWLh) stored (3722 bytes). #metadata/metadata.c:4263 There are 1 physical volumes missing. #device/dev-io.c:308 /dev/sda5: using cached size 3906527232 sectors #metadata/pv_manip.c:421 /dev/sda5 0: 0 63999: root_mimage_0(0:0) #metadata/pv_manip.c:421 /dev/sda5 1: 63999 1: NULL(0:0) #metadata/pv_manip.c:421 /dev/sda5 2: 64000 217600: tristan-home(191155:0) #metadata/pv_manip.c:421 /dev/sda5 3: 281600 191148: tristan-home(0:0) #metadata/pv_manip.c:421 /dev/sda5 4: 472748 4088: swap_1(0:0) #metadata/pv_manip.c:421 /dev/sda5 5: 476836 1: NULL(0:0) #metadata/pv_manip.c:421 /dev/sda5 6: 476837 7: tristan-home(191148:0) #metadata/pv_manip.c:421 /dev/sda5 7: 476844 1: NULL(0:0) #metadata/pv_manip.c:421 /dev/sda5 8: 476845 25: tristan-home(408755:0) #metadata/pv_manip.c:421 /dev/sdb5 0: 0 63999: root_mimage_1(0:0) #metadata/pv_manip.c:421 /dev/sdb5 1: 63999 1: root_mlog_mimage_1(0:0) #metadata/pv_manip.c:421 /dev/sdb5 2: 64000 408781: NULL(0:0) #metadata/pv_manip.c:421 /dev/sdb5 3: 472781 1: root_mlog_mimage_0(0:0) #metadata/pv_manip.c:421 /dev/sdb5 4: 472782 4088: NULL(0:0) #metadata/vg.c:74 Allocated VG tristan at 0x55fd59b64a10. #label/label.c:281 Reading label from lvmcache for /dev/sda5 #label/label.c:281 Reading label from lvmcache for /dev/sdb5 #format_text/import_vsn1.c:597 Importing logical volume tristan/root. #format_text/import_vsn1.c:597 Importing logical volume tristan/swap_1. #format_text/import_vsn1.c:597 Importing logical volume tristan/tristan-home. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mimage_0. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mimage_1. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mlog. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mlog_mimage_0. #format_text/import_vsn1.c:597 Importing logical volume tristan/root_mlog_mimage_1. #metadata/lv_manip.c:1189 Stack tristan/root:0[0] on LV tristan/root_mimage_0:0. #metadata/lv_manip.c:746 Adding tristan/root:0 as an user of tristan/root_mimage_0. #metadata/lv_manip.c:1189 Stack tristan/root:0[1] on LV tristan/root_mimage_1:0. #metadata/lv_manip.c:746 Adding tristan/root:0 as an user of tristan/root_mimage_1. #metadata/lv_manip.c:1189 Stack tristan/root_mlog:0[0] on LV tristan/root_mlog_mimage_0:0. #metadata/lv_manip.c:746 Adding tristan/root_mlog:0 as an user of tristan/root_mlog_mimage_0. #metadata/lv_manip.c:1189 Stack tristan/root_mlog:0[1] on LV tristan/root_mlog_mimage_1:0. #metadata/lv_manip.c:746 Adding tristan/root_mlog:0 as an user of tristan/root_mlog_mimage_1. #metadata/lv_manip.c:746 Adding tristan/root:0 as an user of tristan/root_mlog. #format_text/import.c:198 There are 1 physical volumes missing. #toollib.c:1970 Process single VG tristan #metadata/vg.c:89 Freeing VG tristan at 0x55fd59b68a20. #activate/dev_manager.c:696 Getting device info for tristan-root [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh1U8OpZOZMvZnROK26JsKTnEeRoXFA1IK]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh1U8OpZOZMvZnROK26JsKTnEeRoXFA1IK [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:678 Skipping checks for old devices without LVM- dm uuid prefix (kernel vsn 4 >= 3). #activate/dev_manager.c:696 Getting device info for tristan-swap_1 [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:696 Getting device info for tristan-tristan--home [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley [ noopencount flush ] [16384] (*1) #activate/activate.c:1483 Counted 2 active LVs in VG tristan #vgchange.c:235 2 logical volume(s) in volume group "tristan" already active #activate/dev_manager.c:696 Getting device info for tristan-root [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh1U8OpZOZMvZnROK26JsKTnEeRoXFA1IK]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh1U8OpZOZMvZnROK26JsKTnEeRoXFA1IK [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:696 Getting device info for tristan-swap_1 [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:696 Getting device info for tristan-tristan--home [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:696 Getting device info for tristan-root_mimage_0 [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh0vApwb6YBqJPsfITt1tZG8OXgl1o4ALu]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh0vApwb6YBqJPsfITt1tZG8OXgl1o4ALu [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:696 Getting device info for tristan-root_mimage_1 [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhHtsJVjbdTVDfEaIm5OXvJJkgrK5pUwl2]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhHtsJVjbdTVDfEaIm5OXvJJkgrK5pUwl2 [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:696 Getting device info for tristan-root_mlog [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhSfTj6Bdu0zTX3cxrY9Y6LrDjLJk2RVKv]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhSfTj6Bdu0zTX3cxrY9Y6LrDjLJk2RVKv [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:696 Getting device info for tristan-root_mlog_mimage_0 [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh2xYHUD7D8yvi30OcgMZQZu3KX8wQc601]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh2xYHUD7D8yvi30OcgMZQZu3KX8wQc601 [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:696 Getting device info for tristan-root_mlog_mimage_1 [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhQuUCTPIxuADZeK3AhJSZQkTi4vphwIVh]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhQuUCTPIxuADZeK3AhJSZQkTi4vphwIVh [ noopencount flush ] [16384] (*1) #vgchange.c:242 2 existing logical volume(s) in volume group "tristan" monitored #metadata/lv.c:1535 Activating logical volume tristan/root. #misc/lvm-flock.c:202 Locking /run/lock/lvm/A_tristan WB #misc/lvm-flock.c:100 _do_flock /run/lock/lvm/A_tristan:aux WB #misc/lvm-flock.c:100 _do_flock /run/lock/lvm/A_tristan WB #misc/lvm-flock.c:47 _undo_flock /run/lock/lvm/A_tristan:aux #locking/file_locking.c:104 Locking LV ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh1U8OpZOZMvZnROK26JsKTnEeRoXFA1IK (R) #activate/activate.c:483 activation/volume_list configuration setting not defined: Checking only host tags for tristan/root. #activate/activate.c:2515 Refusing activation of partial LV tristan/root. Use '--activationmode partial' to override. #activate/activate.c:2611 <backtrace> #locking/locking.c:286 <backtrace> #locking/locking.c:358 <backtrace> #misc/lvm-flock.c:70 Unlocking /run/lock/lvm/A_tristan #misc/lvm-flock.c:47 _undo_flock /run/lock/lvm/A_tristan #metadata/lv.c:1537 <backtrace> #toollib.c:1083 <backtrace> #activate/dev_manager.c:696 Getting device info for tristan-root [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh1U8OpZOZMvZnROK26JsKTnEeRoXFA1IK]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh1U8OpZOZMvZnROK26JsKTnEeRoXFA1IK [ noopencount flush ] [16384] (*1) #activate/activate.c:1590 tristan/root is not active #vgchange.c:128 <backtrace> #metadata/lv.c:1535 Activating logical volume tristan/swap_1. #misc/lvm-flock.c:202 Locking /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL WB #misc/lvm-flock.c:100 _do_flock /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL:aux WB #misc/lvm-flock.c:100 _do_flock /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL WB #misc/lvm-flock.c:47 _undo_flock /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL:aux #locking/file_locking.c:104 Locking LV ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL (R) #activate/activate.c:483 activation/volume_list configuration setting not defined: Checking only host tags for tristan/swap_1. #activate/activate.c:2556 Activating tristan/swap_1. #activate/dev_manager.c:696 Getting device info for tristan-swap_1 [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL [ noopencount flush ] [16384] (*1) #activate/activate.c:2567 LV tristan/swap_1 is already active. #misc/lvm-flock.c:70 Unlocking /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL #misc/lvm-flock.c:47 _undo_flock /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL #metadata/lv.c:1535 Activating logical volume tristan/tristan-home. #misc/lvm-flock.c:202 Locking /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley WB #misc/lvm-flock.c:100 _do_flock /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley:aux WB #misc/lvm-flock.c:100 _do_flock /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley WB #misc/lvm-flock.c:47 _undo_flock /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley:aux #locking/file_locking.c:104 Locking LV ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley (R) #activate/activate.c:483 activation/volume_list configuration setting not defined: Checking only host tags for tristan/tristan-home. #activate/activate.c:2556 Activating tristan/tristan-home. #activate/dev_manager.c:696 Getting device info for tristan-tristan--home [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley [ noopencount flush ] [16384] (*1) #activate/activate.c:2567 LV tristan/tristan-home is already active. #misc/lvm-flock.c:70 Unlocking /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley #misc/lvm-flock.c:47 _undo_flock /run/lock/lvm/A_ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley #mm/memlock.c:562 Unlock: Memlock counters: locked:0 critical:0 daemon:0 suspended:0 #activate/fs.c:491 Syncing device names #vgchange.c:155 Activated 2 logical volumes in volume group tristan #vgchange.c:247 <backtrace> #activate/dev_manager.c:696 Getting device info for tristan-root [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh1U8OpZOZMvZnROK26JsKTnEeRoXFA1IK]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLh1U8OpZOZMvZnROK26JsKTnEeRoXFA1IK [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:696 Getting device info for tristan-swap_1 [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhKEuNaNIShSER5P7fTiIwD4mHeXaqS3WL [ noopencount flush ] [16384] (*1) #activate/dev_manager.c:696 Getting device info for tristan-tristan--home [LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley]. #ioctl/libdm-iface.c:1848 dm info LVM-ntPJjDJ0JNBtxHOF1AzkaPBLbhk1vWLhav1jII4xV0UmBevpRG143ysUhsLY2ley [ noopencount flush ] [16384] (*1) #activate/activate.c:1483 Counted 2 active LVs in VG tristan #vgchange.c:253 2 logical volume(s) in volume group "tristan" now active #vgchange.c:774 <backtrace> #toollib.c:1975 <backtrace> #mm/memlock.c:562 Unlock: Memlock counters: locked:0 critical:0 daemon:0 suspended:0 #activate/fs.c:491 Syncing device names #cache/lvmcache.c:157 Metadata cache: VG tristan wiped. #misc/lvm-flock.c:70 Unlocking /run/lock/lvm/V_tristan #misc/lvm-flock.c:47 _undo_flock /run/lock/lvm/V_tristan #device/dev-io.c:625 Closed /dev/sda5 #device/dev-io.c:625 Closed /dev/sdb5 #metadata/vg.c:89 Freeing VG tristan at 0x55fd59b64a10. #metadata/vg.c:89 Freeing VG tristan at 0x55fd59b48410. #libdm-config.c:1061 Setting global/notify_dbus to 1 #lvmcmdline.c:3007 Completed: vgchange -ay -vvvv

Re: Creating a drive mirror with LVM, including exact ...
Thank you for this! Very helpful. It seems that much of the advice out there is still to use the old Linux madam raid, but why do that when LVM can handle it with way more flexibility?
One comment: you might want to add a few extra arguments to the lvconvert command, to guard against unwieldy wait times after a system crash, as the mirrors rebuild:
I found that tidbit here: http://www.sandelman.ca/mcr/blog/lvm/
Cheers