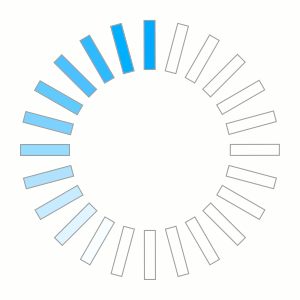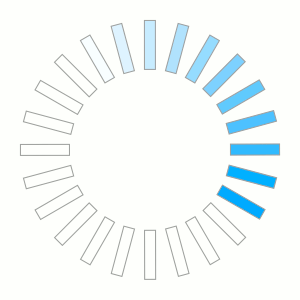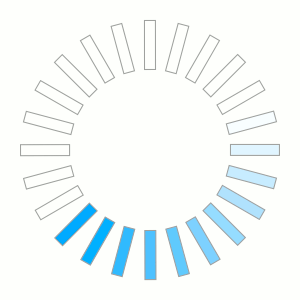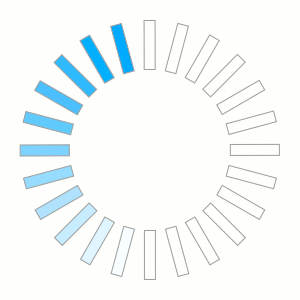As I'm working on a new feature for our Snap! Website system I wanted to have a turning wheel that asks users to wait while the computer does work.

The graphic is very simple: a rectangle with a border and a background color that rotates. However, I do not have a tool (that I know of) which could create the graphics automatically. So I did it with quite a bit of manual labor, but it was fun to learn a few things along the way.

I use inkscape to create such graphics. First I created the rectangle on the left. With that I had to have it rotated going 360 degrees repeating the rectangle 24 times.

The image is 300x300 pixels. Since inkscape works with SVG it offers a way to apply a transformation on any object. So, all I had to do is duplicate the first rectangle and then rotate by 15° it to the next position. With the system, you have to move the center of rotation (you see it appearing after you clicked on the shape a second time.)

Now to do that faster you want to calculate a matrix that moves the rectangle by 15° or -15° and apply that matrix over and over again. The matrix gives you a very close result. Closer than doing it 24 times by hand.

I wrote a quick C++ program using Boost and ublas (all of that is available as is under Linux) and compiled it and ran it. The result here is:

Result: [3,3]((0.965926,-0.258819,43.934),(0.258819,0.965926,-33.7117),(0,0,1))

As you can see the last part of the matrix is (0, 0, 1) which is good because you cannot enter that row in InkScape. So if you generate a matrix which does not end up that way, it is likely not going to work well.

#include <boost/numeric/ublas/matrix.hpp>
#include <boost/numeric/ublas/io.hpp>

using namespace boost::numeric::ublas;

main()
{
    matrix<double> p(3, 3); // start with identity
    p(0, 0) = 1.0;
    p(1, 1) = 1.0;
    p(2, 2) = 1.0;

    matrix<double> m1(3, 3); // translate (-150, -150)
    m1(0, 0) = 1.0;
    m1(0, 1) = 0.0;
    m1(0, 2) = -150.0;
    m1(1, 0) = 0.0;
    m1(1, 1) = 1.0;
    m1(1, 2) = -150.0;
    m1(2, 0) = 0.0;
    m1(2, 1) = 0.0;
    m1(2, 2) = 1.0;
    p = prod(m1, p);

    matrix<double> m2(3, 3); // rotate by alpha
    double alpha = 30.0 * M_PI / 360.0;
    m2(0, 0) = cos(alpha);
    m2(0, 1) = -sin(alpha);
    m2(1, 0) = sin(alpha);
    m2(1, 1) = cos(alpha);
    m2(2, 2) = 1.0;
    p = prod(m2, p);

    matrix<double> m3(3, 3); // translate (150, 150)
    m3(0, 0) = 1.0;
    m3(0, 1) = 0.0;
    m3(0, 2) = 150.0;
    m3(1, 0) = 0.0;
    m3(1, 1) = 1.0;
    m3(1, 2) = 150.0;
    m3(2, 0) = 0.0;
    m3(2, 1) = 0.0;
    m3(2, 2) = 1.0;
    p = prod(m3, p);

    std::cout << "Result: " << p << "\n";
}

With that result I would duplicate a rectangle, apply the matrix, duplicate that rectangle (Ctrl-D), apply the matrix, etc.  Since the matrix rotates the rectangle by 15° the process can be repeated 23 times to get the 24 rectangles.

Once that is done, you have to add the colors to a few rectangles. Finally, selecting the 24 rectangles you can then rotate the whole thing 15°. Do that 24 times and you've got the 24 images that rotate.

I save all of those as GIF images and then assembled the result with gifsicle (also available as is under Linux.)